Hay diferentes tipos de discontinuidades:
- Discontinuidad evitable: si el límite existe pero no es igual a f(a).
Ejemplo 1:
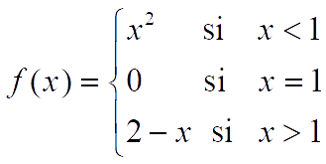
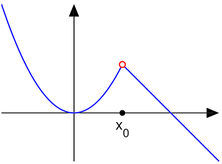f tiene una discontinuidad evitable en x = 1
–Discontinuidad inevitable: cuando existen los límites laterales y no son iguales. Puede ser salto finito o infinito
Ejemplo 2:
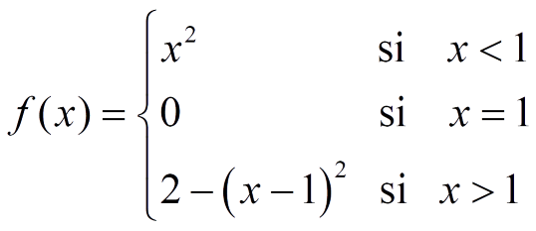
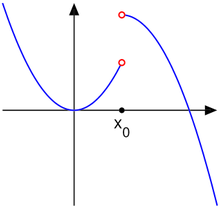f tiene una discontinuidad inevitable en x = 1, con salto 1
Ejemplo 3:
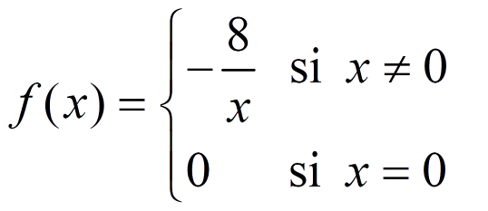
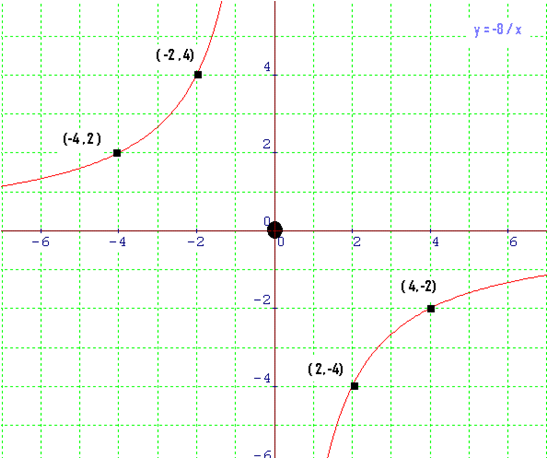f tiene una discontinuidad inevitable con salto infinito en x = 0
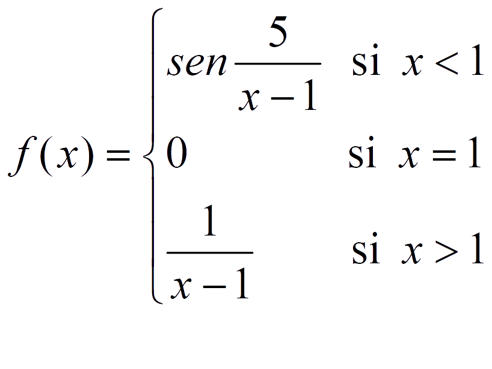
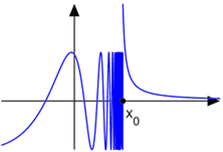
Ejercicios
1.- Estudia la continuidad de estas funciones y clasifica sus discontinuidades, si las tienen:
2.- Estudia la continuidad de esta función en según los valores de a:
Soluciones:
1.- a) f es continua en R-{-1}, en x = -1 f tiene una discontinuidad inevitable con salto (e - 2); b) g es continua en R
2.- Si a = -1, f es continua en R
- Si a ≠ -1, f es continua en R-{2}, en x = 2 f tiene una discontinuidad inevitable con salto (3 + 3a)