- i) det(A) = det(At). Entonces todas las propiedades para filas los son también para columnas.
- ii) Si cambiamos dos filas o columnas el signo del determinante cambia:
![]()
En consecuencia, si hacemos un número impar de cambios el determinante cambia de signo, y si ese número es par no cambia.
Ejemplo:
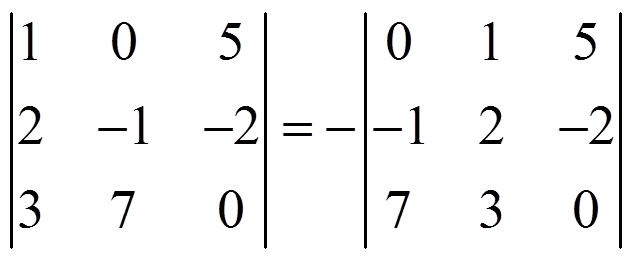
- iii) Si multiplicamos una fila o una columna por un número, el determinante queda multiplicado por ese número:
Ejemplo:
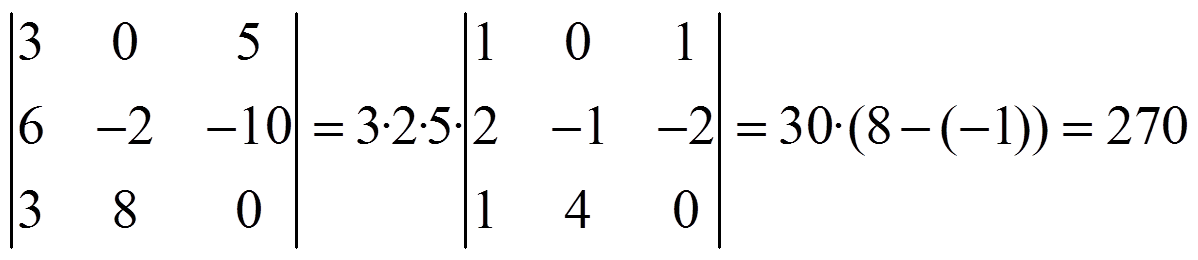
- iv)
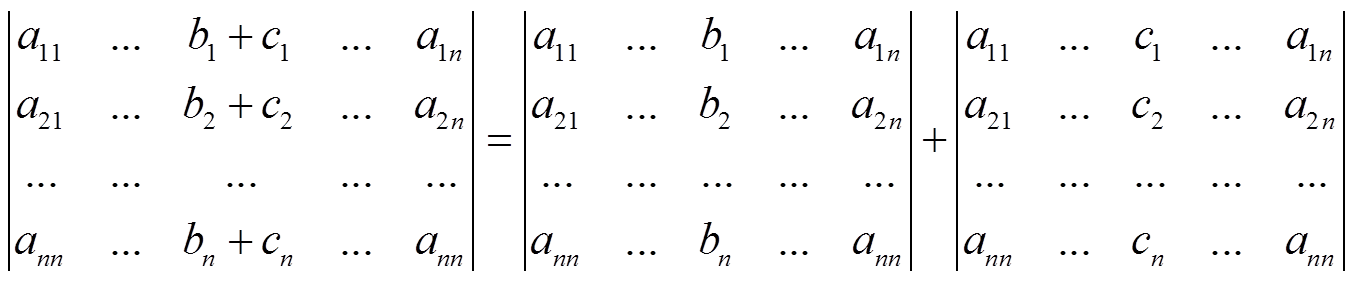
Análogo para filas
Demostración: si desarrollamos el determinante por esta columna:
|A|= A1j(b1 + c1) +…= A1j·b1+…+A1j·c1 QED
- v) Si A tiene una fila o columna de ceros, el determinante es 0
- vi) Si A tiene dos filas o columnas iguales → |A| = 0
Demostración: supongamos que Fi = Fj
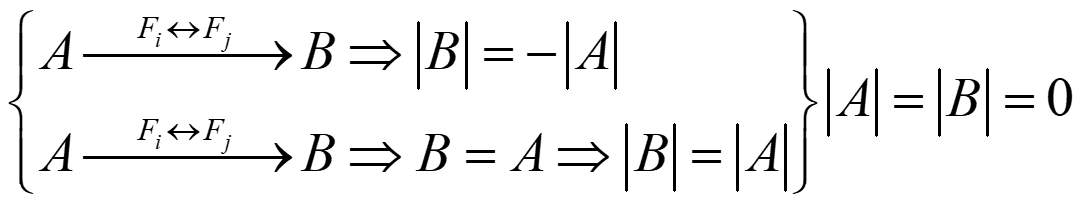
- vii) Si A tiene dos filas o columnas proporcionales→ |A| = 0
- viii) Si añadimos una fila por un número, k·Fi , a otra fila, Fj, el determinante no cambia.
Demostración: |A| = |…Fi…Fj…|
|...Fi…Fj+kFi…| = |..Fi…Fj…|+ |..Fi…kFi…| = |A|
- ix) |A·B| = |A|·|B|
NOTAS:
- 1) Si todos los elementos de una fila o columna son cero excepto uno, el determinante es el producto de ese elemento por su adjunto.
- 2) Si la matriz es triangular o diagonal, el determinante es el producto de los elementos de la diagonal.
- 3) Si una fila o columna es combinación lineal de las otras (Fi = k1F1+k2F2+…)→ |A| = 0
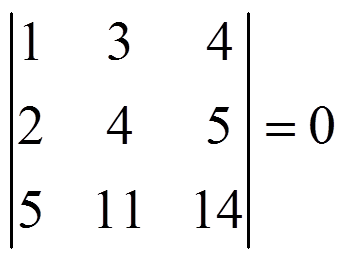
Ejemplos:
1) Si
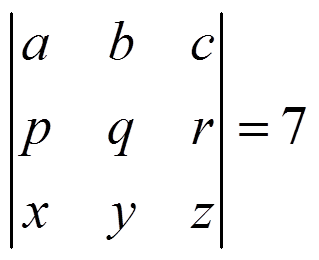
calcula:
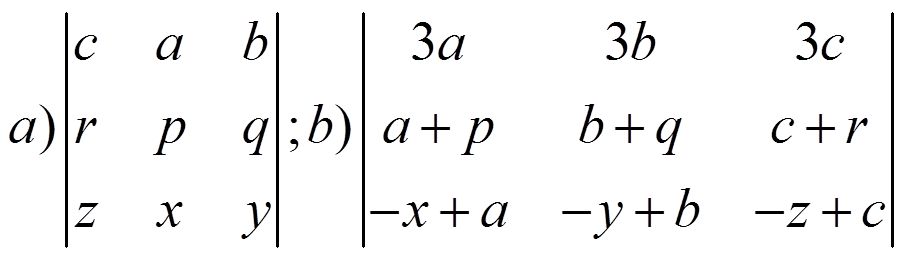
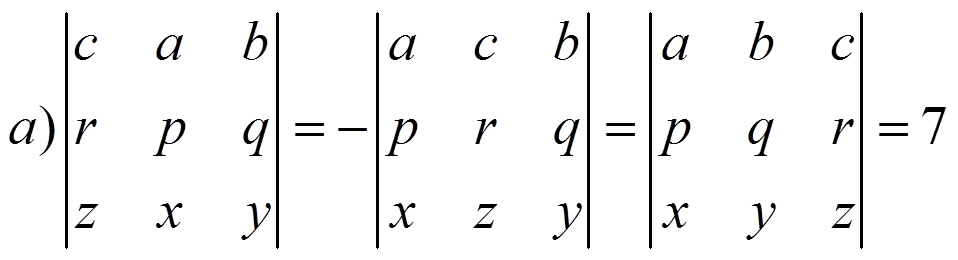
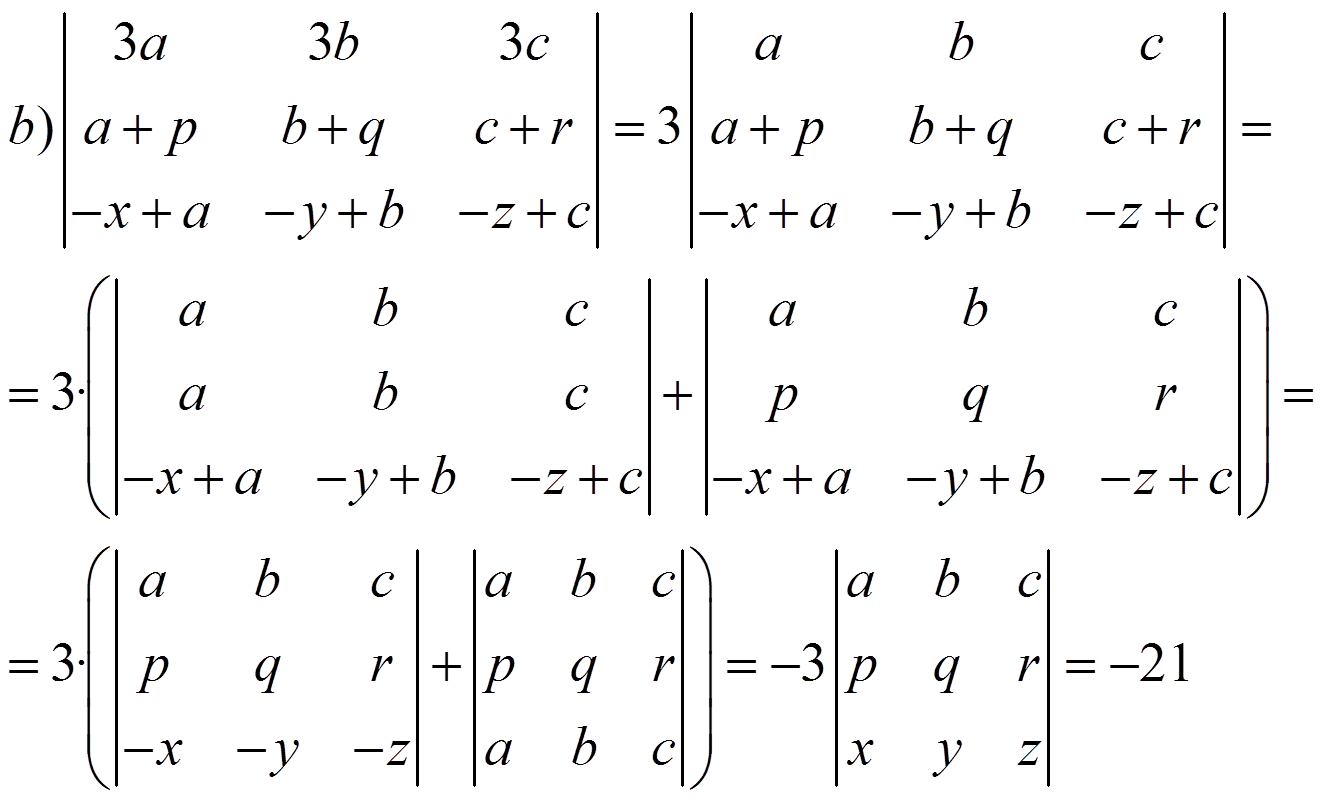
2) Resuelve:
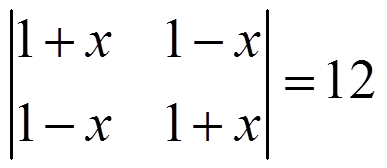
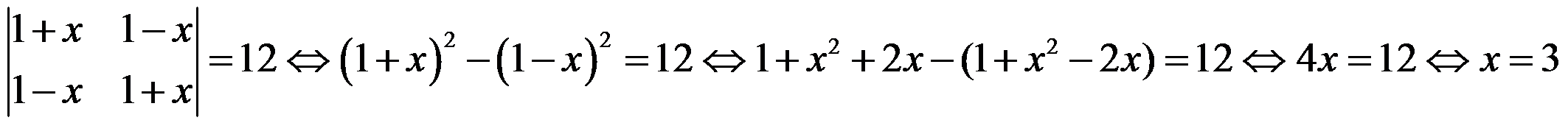
3) Resuelve:
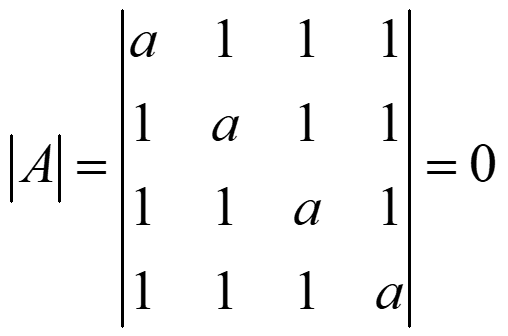
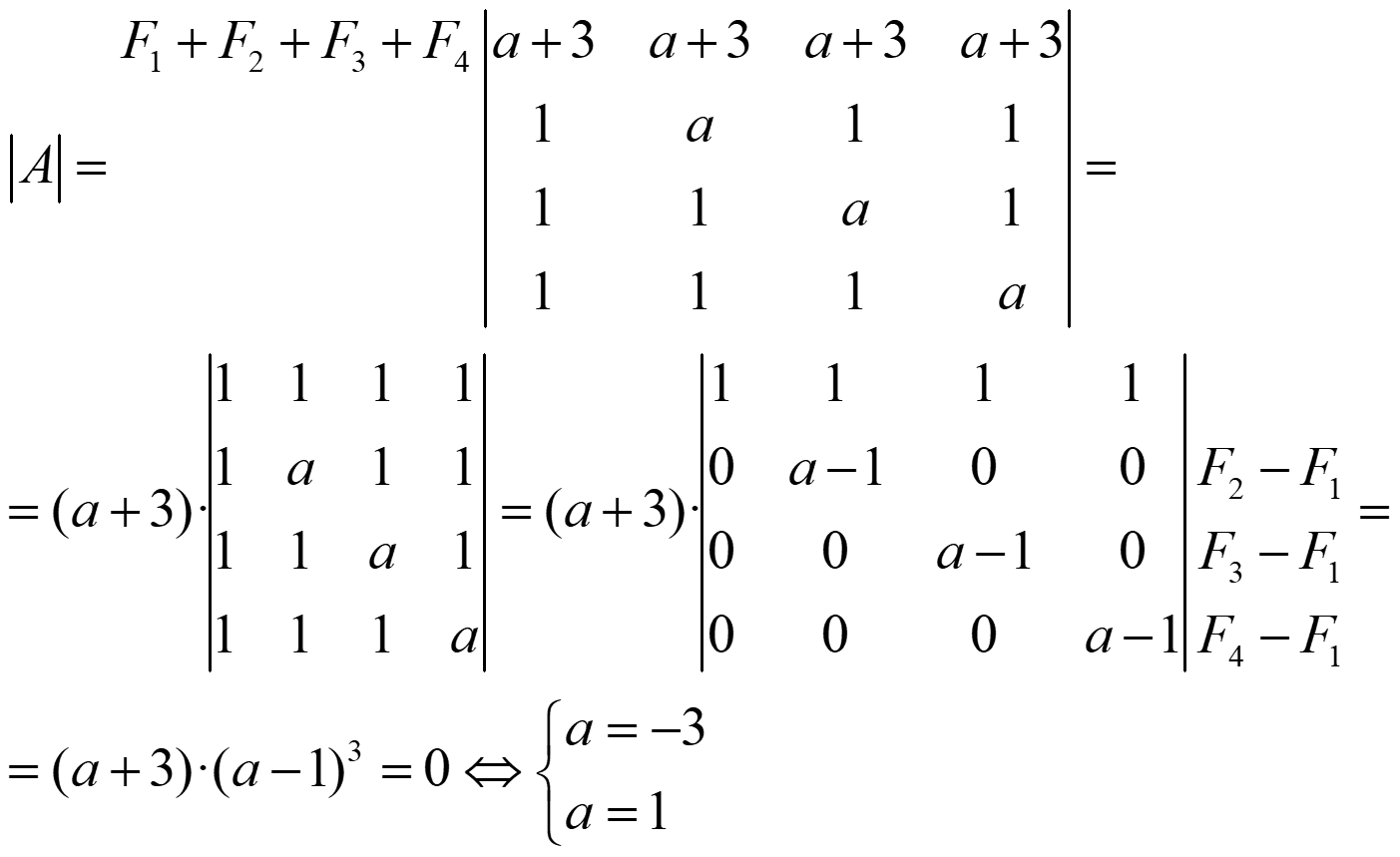
Ejercicios
1.- Calcula:
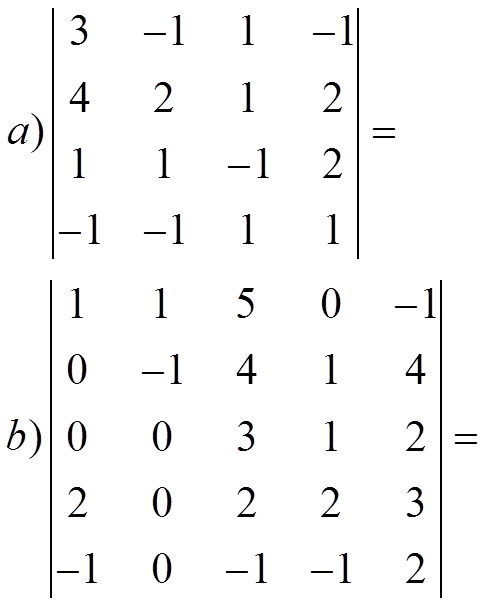
2.- Resuelve:
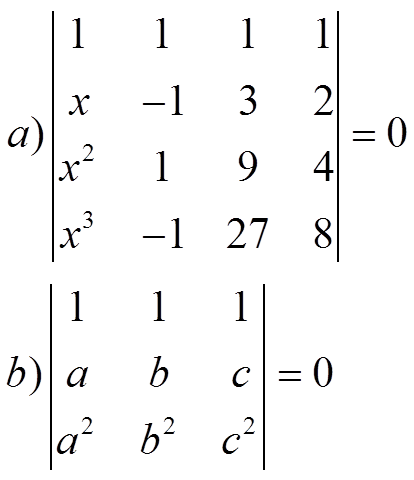
3.- Si
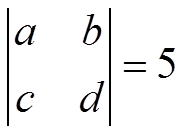
calcula:
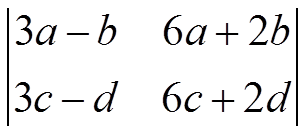
Soluciones: 1) a) -36; b) -56; 2) a) x € {-1,2,3}; b) a=b, b=c, a=c; 3) 60