- Razones de las sumas de ángulos:
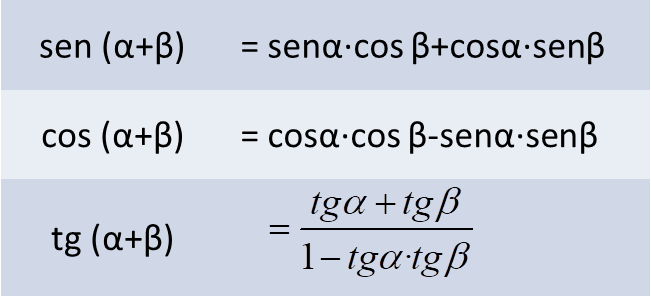
Ejemplo:
![]()
\[sen{{75}^{o}}=sen\left( {{45}^{o}}+{{30}^{o}} \right)=sen{{45}^{o}}\cdot \cos {{30}^{o}}+\cos {{45}^{o}}\cdot sen{{30}^{o}}=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot \frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}\]
- Razones de la resta de ángulos:
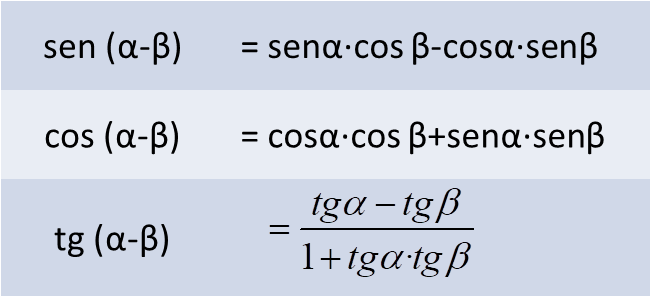
Ejemplo:
![]()
\[sen{{15}^{o}}=sen\left( {{45}^{o}}-{{30}^{o}} \right)=sen{{45}^{o}}\cdot \cos {{30}^{o}}-\cos {{45}^{o}}\cdot sen{{30}^{o}}=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}\cdot \frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}\]
- Razones del ángulo doble
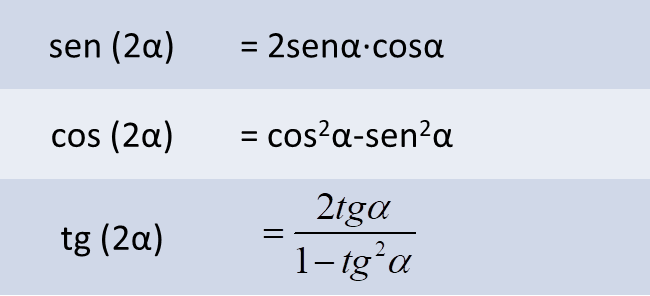
Ejemplo:
![]()
\[sen{{60}^{o}}=sen\left( 2\cdot {{30}^{o}} \right)=2sen{{30}^{o}}\cos {{30}^{o}}=2\cdot \frac{1}{2}\cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}\]
- Razones del ángulo mitad:
![]()
Ejemplo:
![]()
\[sen{{15}^{o}}=sen\frac{{{30}^{o}}}{2}=+\sqrt{\frac{1-\cos {{30}^{o}}}{2}}=\sqrt{\frac{1-\frac{\sqrt{3}}{2}}{2}}=\sqrt{\frac{2-\sqrt{3}}{4}}=\frac{\sqrt{2-\sqrt{3}}}{2}\]
Ejercicios:
1.- Calcula usando las fórmulas:
a) tg 75o
b) cos 15o
c) sen 90o (usando que 90o = 2·45o)
2.- Verifica estas identidades:
![]()
\[a)se{{n}^{2}}\left( \frac{x}{2} \right)=\frac{1-{{\cos }^{2}}x}{4{{\cos }^{2}}\left( \frac{x}{2} \right)}\quad \quad \quad b)\frac{\cos (a+b)-\cos (a-b)}{sen(a+b)+sen(a-b)}=-tgb\]
Soluciones: a) 2 + √3; b) (√6+√2)/4; c) 1