El producto escalar de dos vectores, u y v, es el número:
![]()
Ejemplo:
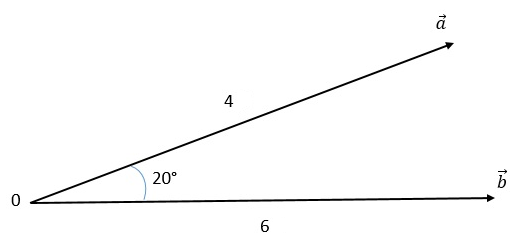
![]()
Propiedades:
- u · u = |u|2 ≥ 0
- u · v = v · u
- λ · u · v = (λu)·v = u·(λv) λ€ R
- u·(v + w) = u · v + u · w
- Se dice que dos vectores son ortogonales si u · v = 0. Entonces: u y v son ortogonales ↔ forman un ángulo de 90o
NOTA: un vector ortogonal a u(u1,u2) es (-u2,u1)
Interpretación geométrica del producto escalar:
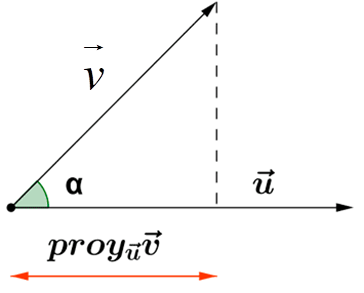
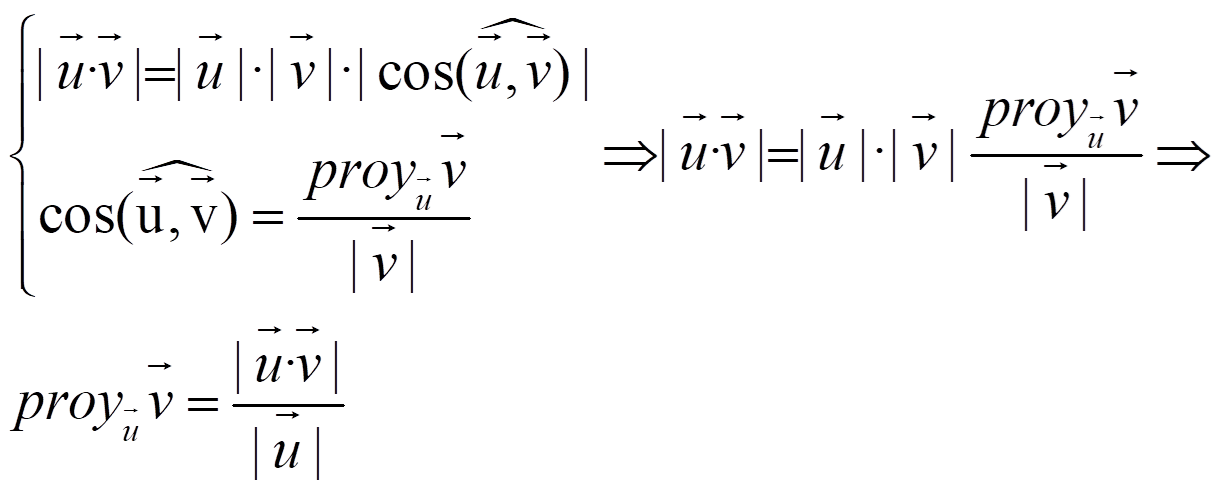
Ejercicio. Dados u y v en la figura, calcula u·v y proyuv
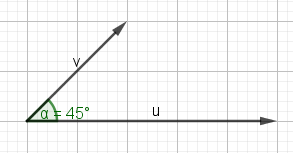
Soluciones: u·v=10; proyuv=2u