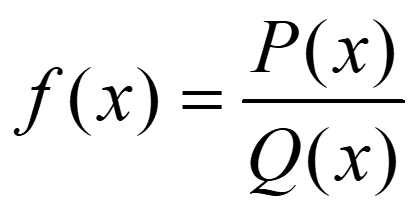
- I) Si gradoP ≥ gradoQ, tenemos que dividir y descomponer:
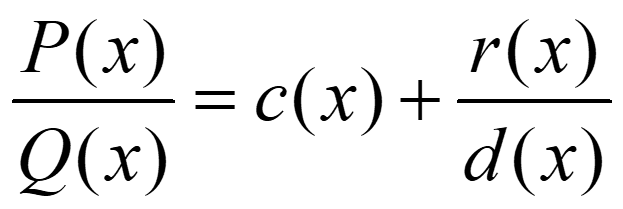
c(x) = cociente; r(x) = resto
Entonces tenemos: polinomio + integral inmediata o caso II
- II) Si gradoP < gradoQ, tenemos tres casos:
- Q sólo tiene raíces reales simples
- Q tiene raíces reales múltiples
- Q tiene raíces complejas
- II.a) Q(x) = a·(x – x1)·(x – x2)·…
Entonces, tenemos que buscar A1, A2,…Є R, tales que:
![]()
y tendremos integrales inmediatas (ln)
Ejemplo:
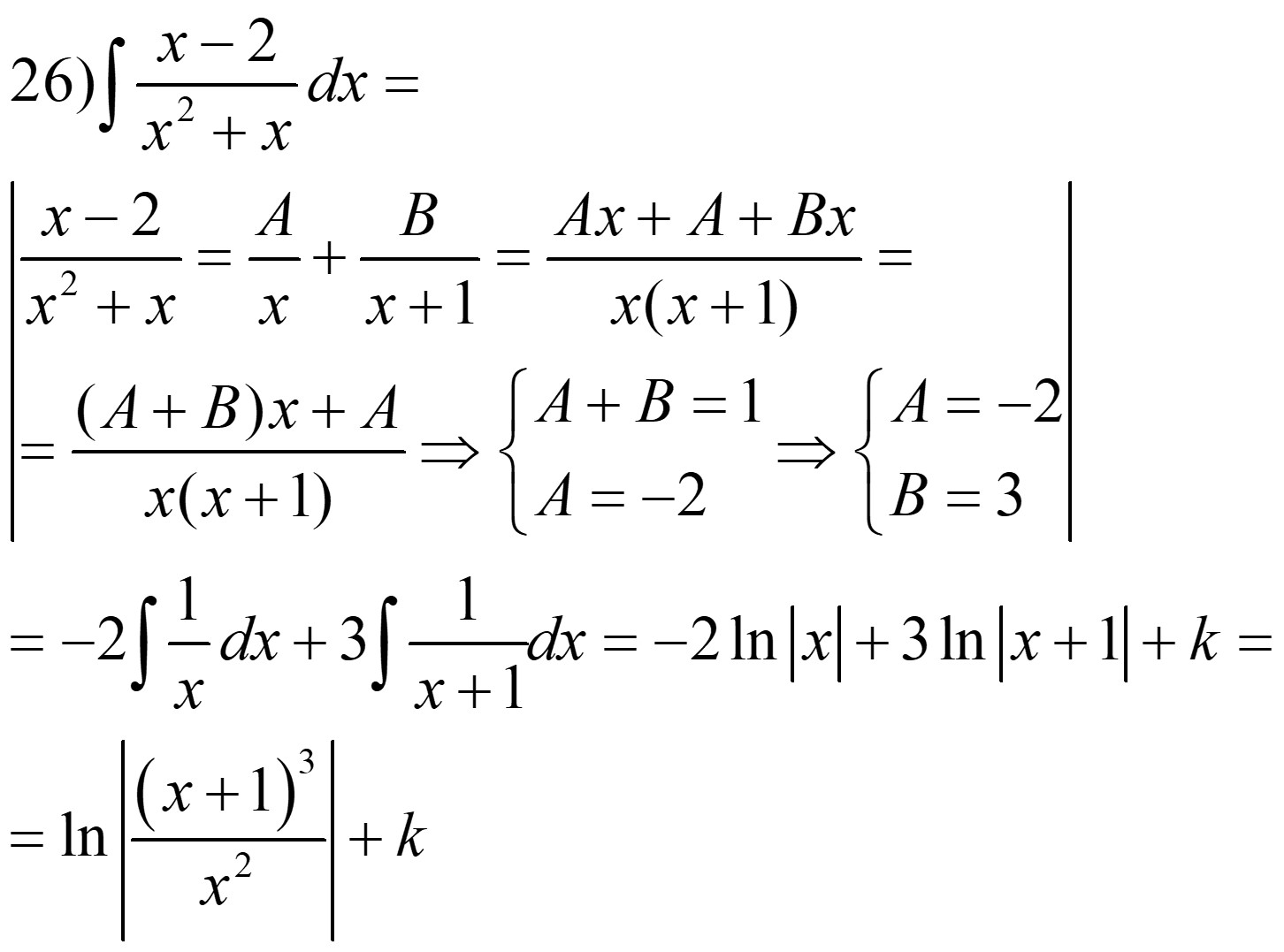
- II.b) Q(x) = (x – x1)n ·…
Entonces, tenemos que buscar A1, A2,…,AnЄ R, tales que:
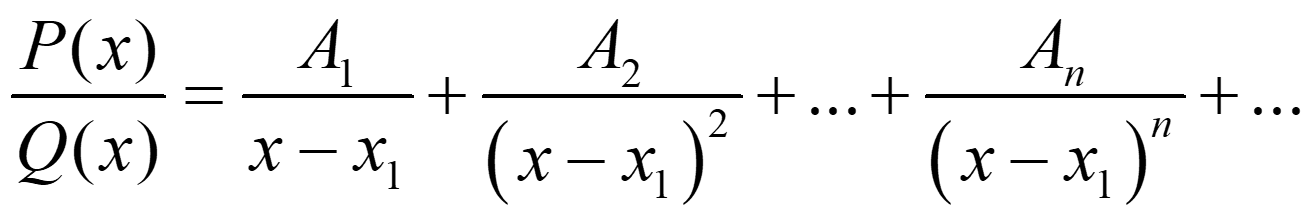
y tendremos, de nuevo, integrales inmediatas
Ejemplo:
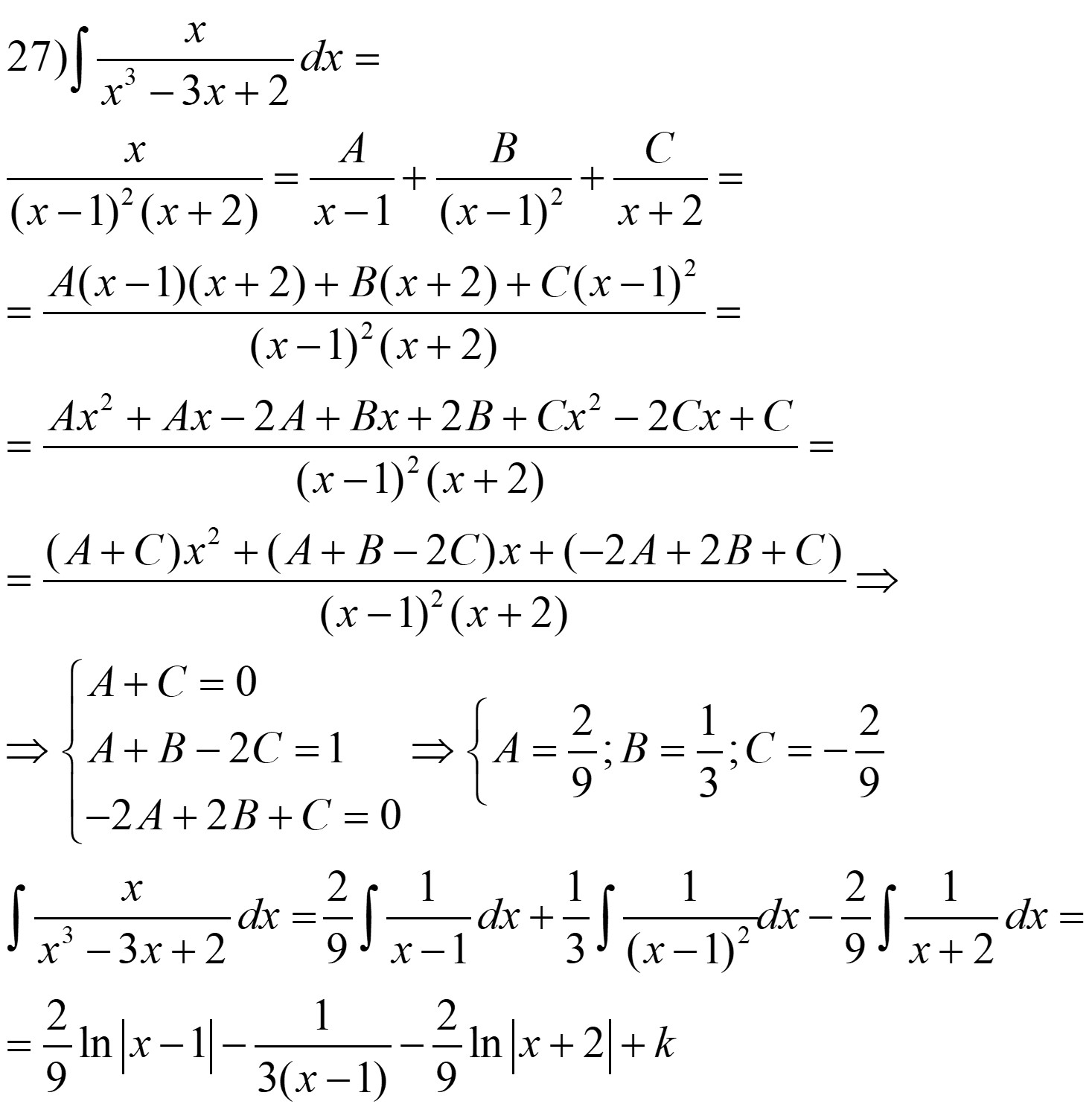
- II.c) Q(x) = (ax2 + bx + c)·…
Entonces, tenemos que buscar M,NЄ R, tales que:
![]()
y tendremos integrales inmediatas (ln + arctg)
Ejemplo:
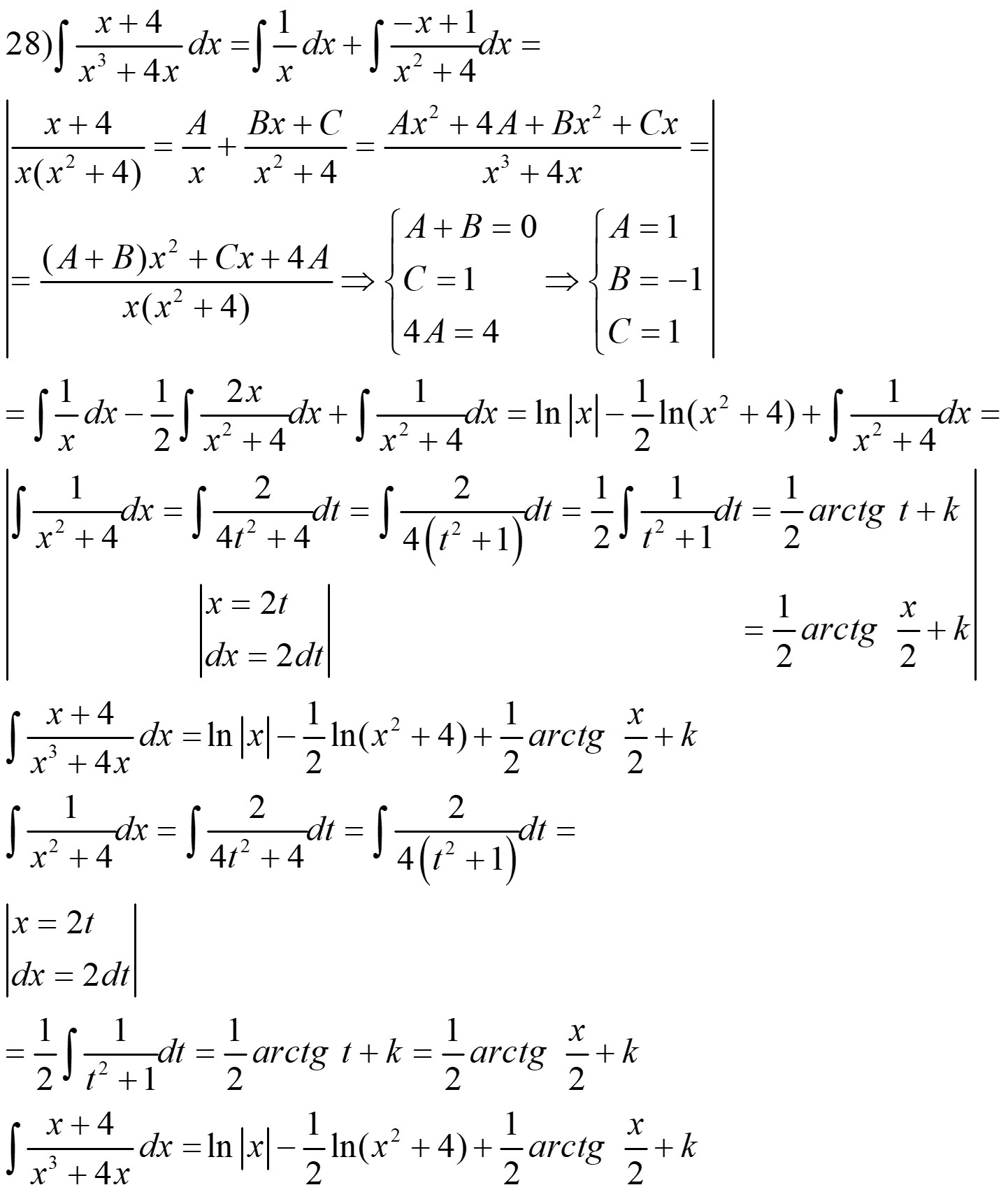
Ejercicio. Resuelve las siguientes integrales
 :
:
Soluciones:
