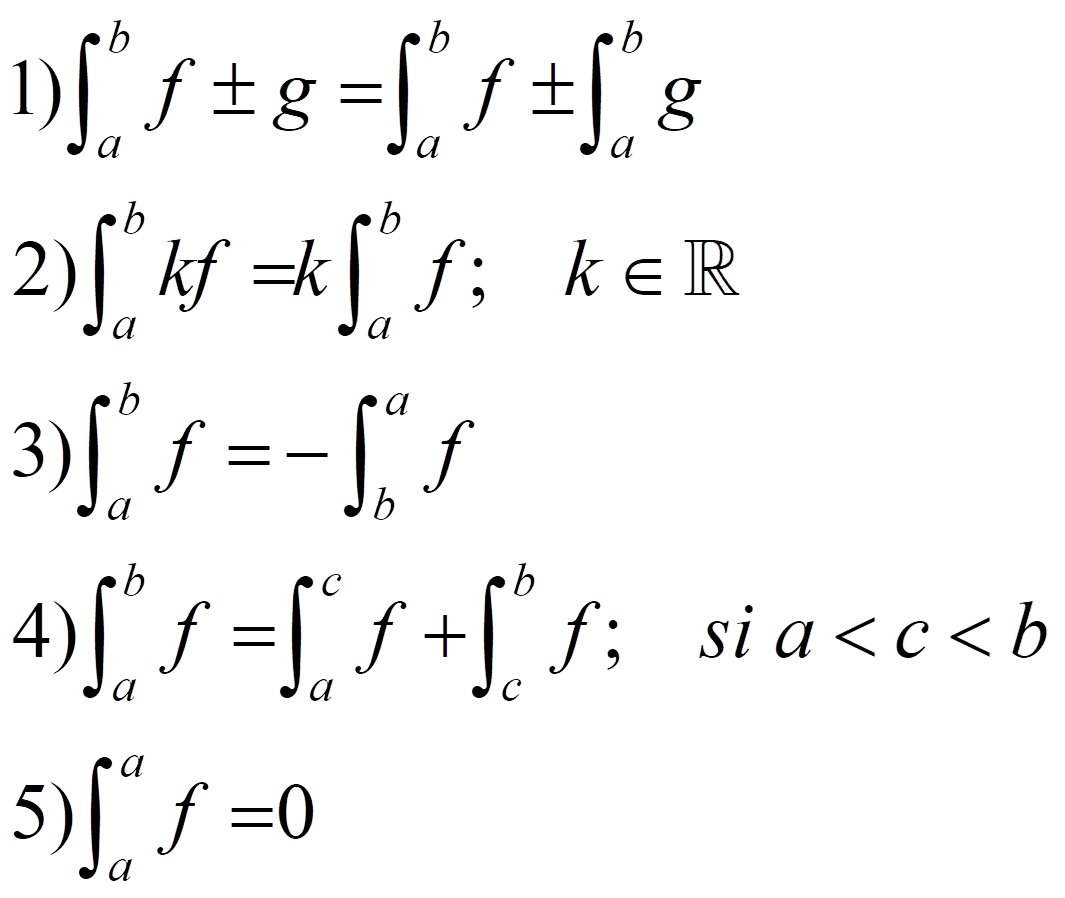Vamos a calcular el área bajo la gráfica de una función en un intervalo, el área de R.

Para conseguirlo, hacemos una partición, Pn, del intervalo [a,b] en n subintervalos:
a = x0<x1<x2<……<xn = b
Entonces, tenemos dos opciones para calcular el área:
- La suma inferior de f asociada a la partición Pn, (área inferior) sPn(f)

- La suma superior de f asociada a la partición Pn, (área superior) SPn(f)

Obviamente:
sPn(f)≤ área (R) ≤ SPn(f)
Si elegimos otra partición, Pn’, n’ > n, entonces:


sPn(f)≤ sPn’(f)≤ área (R) ≤ SPn’(f) ≤ SPn(f)
Si hacemos el límite cuando n tiende a ∞ y ambos son iguales, entonces:
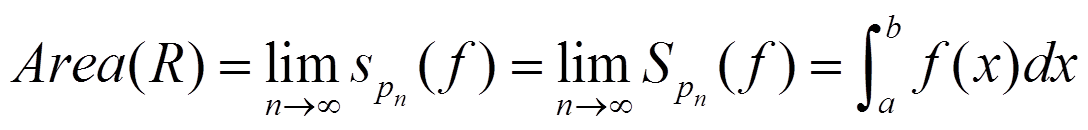
se llama integral definida de f entre a y b, y se dice que f es integrable en [a,b]
PROPIEDADES: