TEOREMA. Si una función f es derivable en x = a, entonces f es también continua en x = a.
Demostración: tenemos que probar que
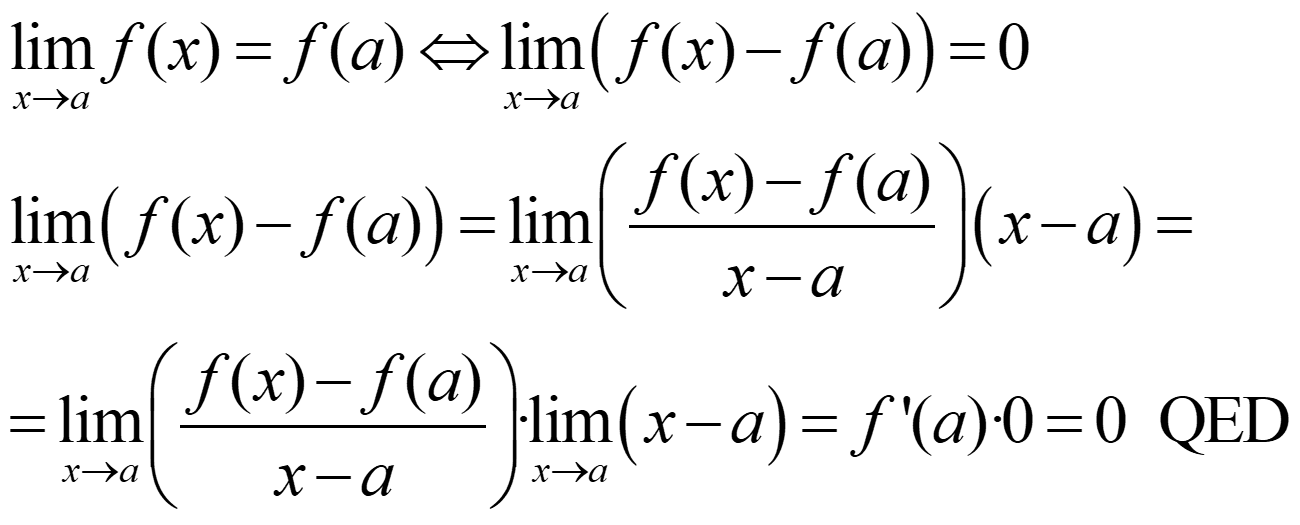
NOTA. No todas las funciones continuas son derivables en x = a.
Ejemplo. f(x) = |x| en x = 0
Como se puede observar, la derivabilidad implica curvas suaves y la no derivabilidad picos.
Definimos la función derivada como:
Sólo tenemos que estudiar la derivabilidad en los puntos en los que la función es continua. En esos puntos tenemos que comprobar que los límites laterales (derivadas laterales) son iguales: f’(a-) = f’(a+) (derivada izquierda = derivada derecha).
Ejemplo:
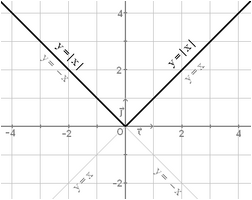
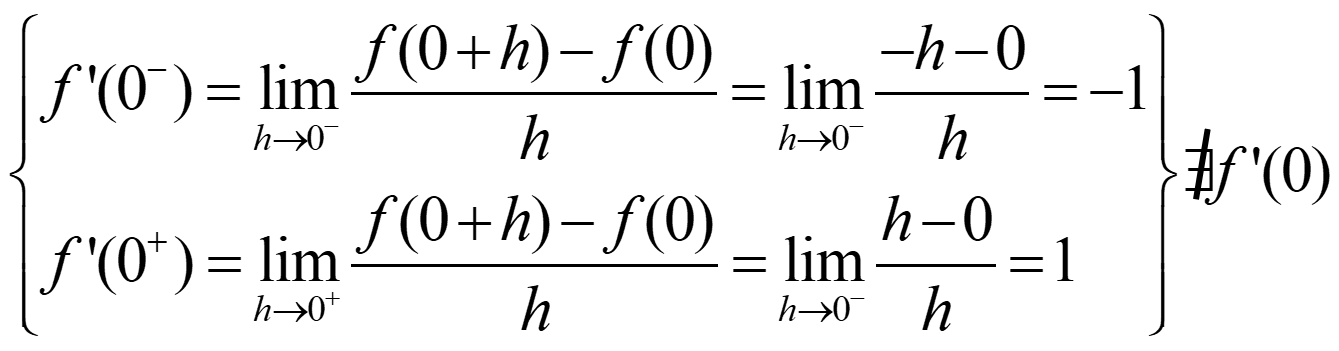
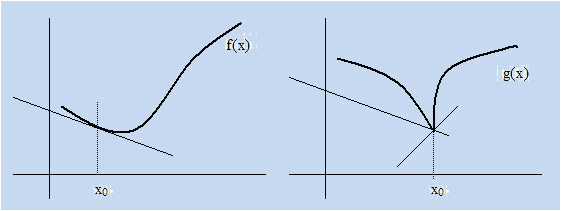
Ejemplo:
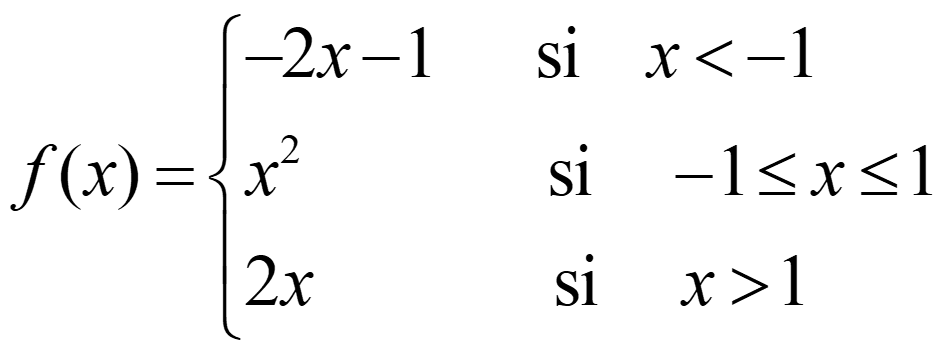f es derivable en R-{1}
Ejercicios
1.- Encuentra la derivada de las funciones:
2.- Encuentra la abscisa en la cual la pendiente de la tangente a la gráfica de la función f(x) = x2 + 1 es 6.
3.- Estudia la derivabilidad de:
4.- Encuentra los valores de a y b que hacen que la función
sea continua y derivable en R.
Soluciones: 1. f'(x) = -2/x2; b) f'(x) = 2x; 2. x = 3; 3. f es derivable en R; 4. a = 2, b = -1