La tasa de variación de una función f en un intervalo [x1,x2] es: TV = f(x2) – f(x1)
La tasa de variación media de una función en un intervalo [x1,x2] es
![]()
Ejemplo. f(x) = x2
![]()
Si f es decreciente en el intervalo, entonces TVM < 0; si es creciente, entonces TVM > 0
Si f es constante, entonces TVM = 0
Sea f definida en un intervalo abierto centrado en a, la derivada, f’(a), de la función f en x = a es el límite:
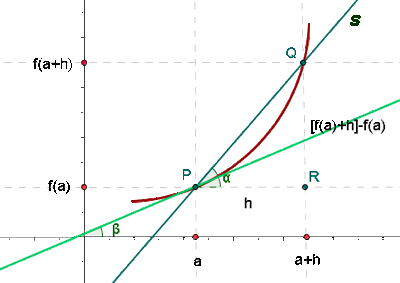
Cuando la función es continua y el límite existe, decimos que f es derivable en x = a.
Como se observa, la derivada es la pendiente de la recta tangente a la curva en el punto.
También se le llama tasa de variación instantánea.
Como se observa, la derivada es la pendiente de la recta tangente a la curva en el punto.
También se le llama tasa de variación instantánea.
La ecuación de la recta tangente a la curva en ese punto es entonces:
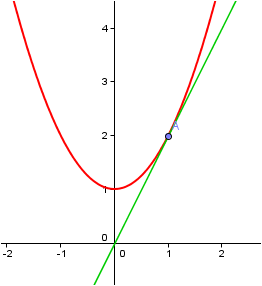
Ejemplo. Si f(x) = x2 + 1, calcula f’(1) y la recta tangente a la curva en ese punto.
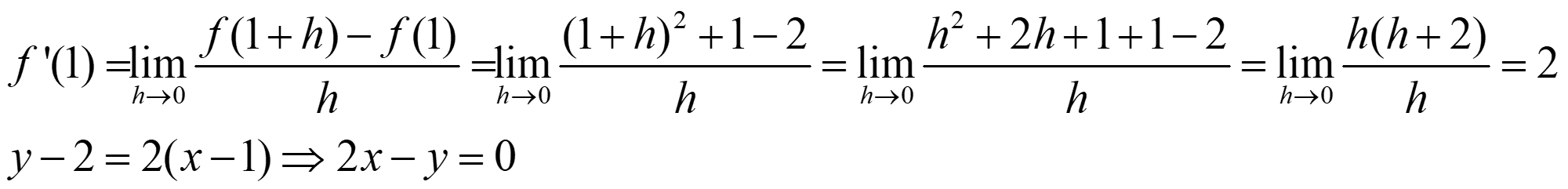
Ejercicios
1) Calcula la tasa de variación media de estas funciones en los intervalos.
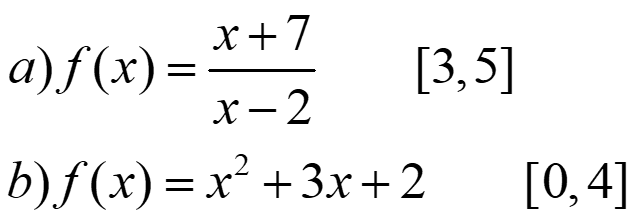
2) Calcula la derivada de las funciones en esos puntos, usando la definición:
a) f(x) = x + 7 en x = 3
b) f(x) = x2 + x en x = 2
Soluciones:1) a) -3; b) 1; 2) a) 1; b) 5