4. simetría

Una función es par si f(-x) = f(x), es decir, es simétrica respecto al eje Y:

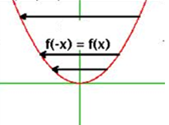
Una función es impar si f(-x) = -f(x), es decir, es simétrica respecto al origen:

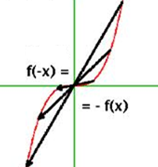
Ejemplo 1: f(x) = x⁴ - x² es una función par porque f(-x) = (-x)⁴ – (-x)² = x⁴ – x² = f(x)

Ejemplo 2: f(x) = x³ es impar porque f(-x) = (-x)³ = - x³ = -f(x)

Ejemplo 3: f(x) = x³ – 3 no es ni par ni impar porque:

f(-x) = (-x)³ - 3 = -x³ – 3 ≠ -f(x)

Ejercicio. Estudia la simetría de estas funciones:

a) f(x) = x⁴ + 3x² - 7

b) f(x) = x⁵ - x³ + x - 7

Soluciones: a) par: b) ni par ni impar; c) impar