Funciones
8. extremos, crecimiento y decrecimiento
Se dice que una función es creciente en un intervalo si, para todo x1 y x2 en el intervalo tal que x1 < x2, entonces f(x1) < f(x2).
Se dice que una función es decreciente en un intervalo si, para todo x1 y x2 en el intervalo tal que x1 < x2, entonces f(x1) > f(x2).
El máximo y mínimo de una función, los extremos, son el valor mayor y menor que toma la función en un punto bien en un entorno dado (extremo relativo) o en todo el dominio (extremo absoluto).
Ejemplos: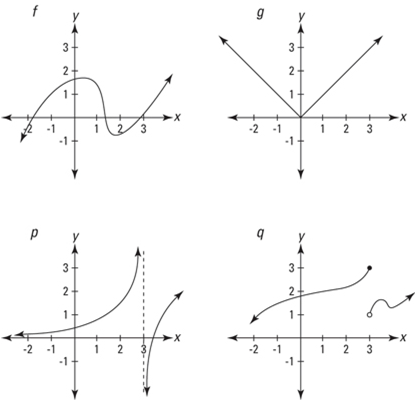
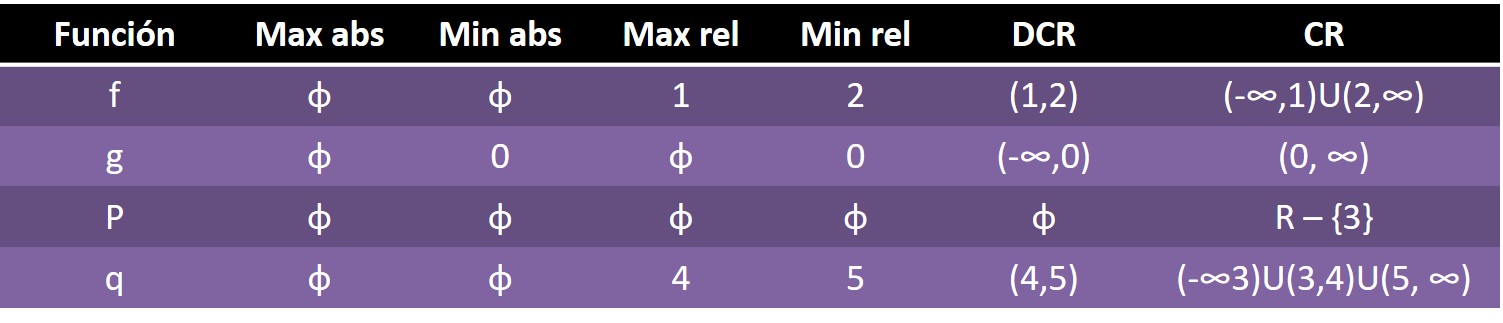
Ejercicio. Estudia el crecimiento, decrecimiento, máximos y mínimos de las siguientes funciones:
a) 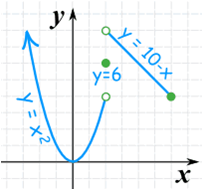
b) 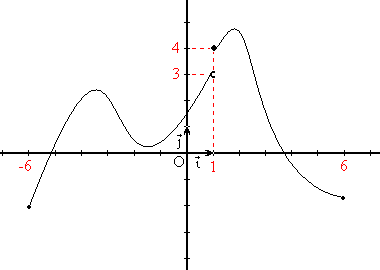
Soluciones:
| función | max abs | min abs | max rel | min rel | crecimiento | decreciente |
| a) | Φ | 0 | Φ | 0 | (0,2) | (-∞,0)U(2,6) |
| b) | 2 | -6, 6 | -3.5 , 2 | -1.5 | (-6,-3.5)U(-1.5,2) | (-3.5,-1.5)U(2,6) |
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0