Funciones afines

Una función es afín si tiene esta expresión algebraica: y = f(x) = mx + n (m,n є R), con un polinomio de grado 0 o 1.

Su gráfica es una recta, donde m se llama pendiente y n ordenada en el origen.

• Si m > 0 la función es creciente

• Si m < 0 la función es decreciente

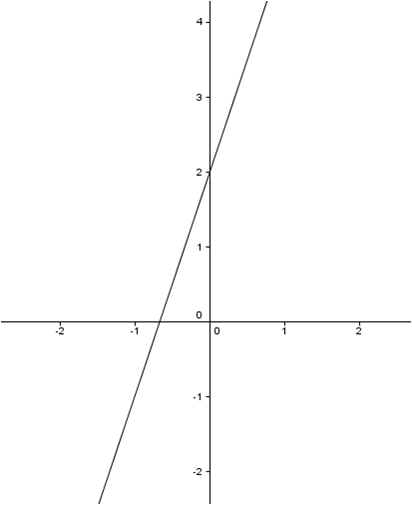
Ejemplo: f(x) = 3x + 2

Si tenemos o bien 2 puntos o un punto y la pendiente de una función afín, podemos encontrar su expresión algebraica.

Con dos puntos, calculamos m a partir del vector que los une y obtenemos n sustituyendo un punto en la fórmula.

Con un punto y la pendiente, obtenemos n como antes.

Ejemplo: si tenemos dos puntos (1,1) y (3,4):

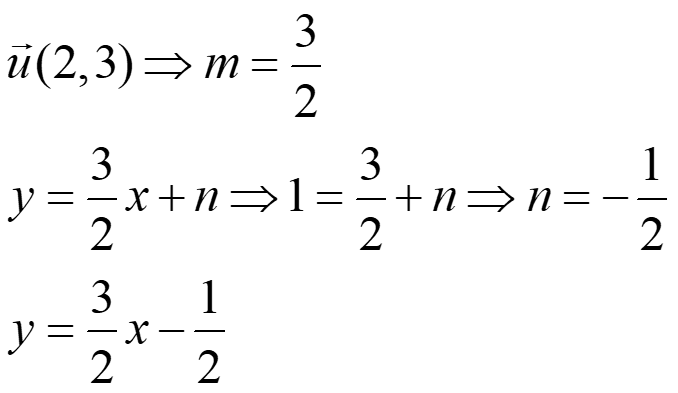
Ejercicio. Averigua la ecuación de la recta que:

a) pasa por los puntos (1,1) y (3,3)

b) pasa por el (1,0) y tiene pendiente -2

Soluciones: a) y = x; b) y = -2x + 2