Ejemplos | Rectas y planos en el espacio

Ejemplo 1. Encuentra el plano π y una recta s que pasen por el punto (5,5,1) y sean perpendiculares a r:

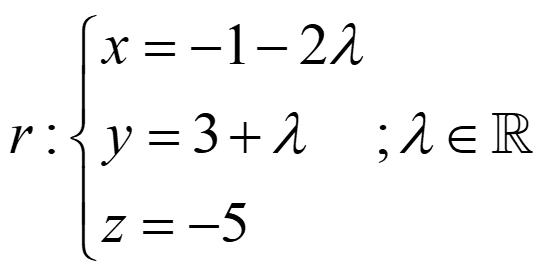
Todas las rectas de π son perpendiculares a r, por ejemplo:

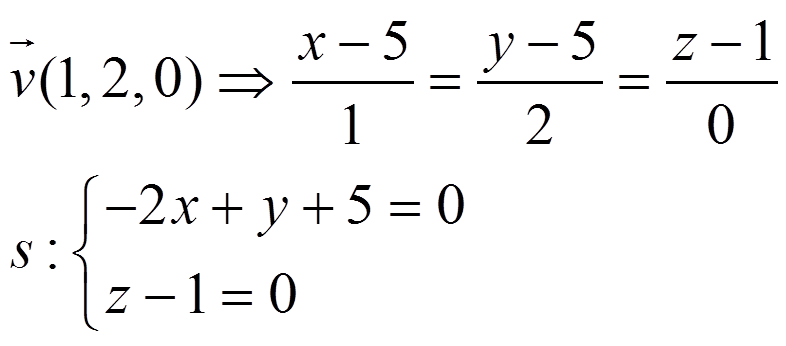
Ejemplo 2. Encuentra el plano π que contiene a r y s:

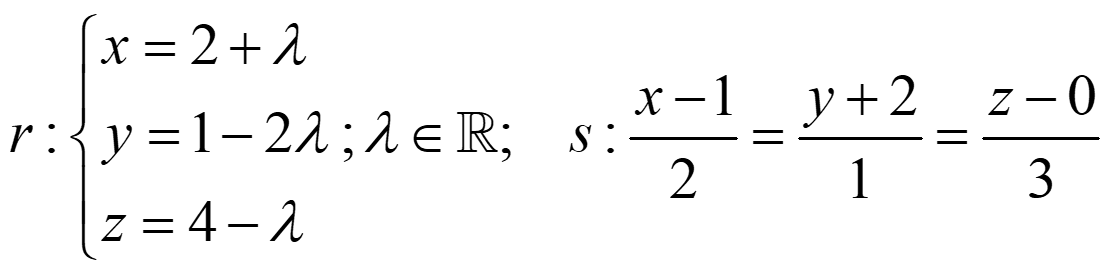
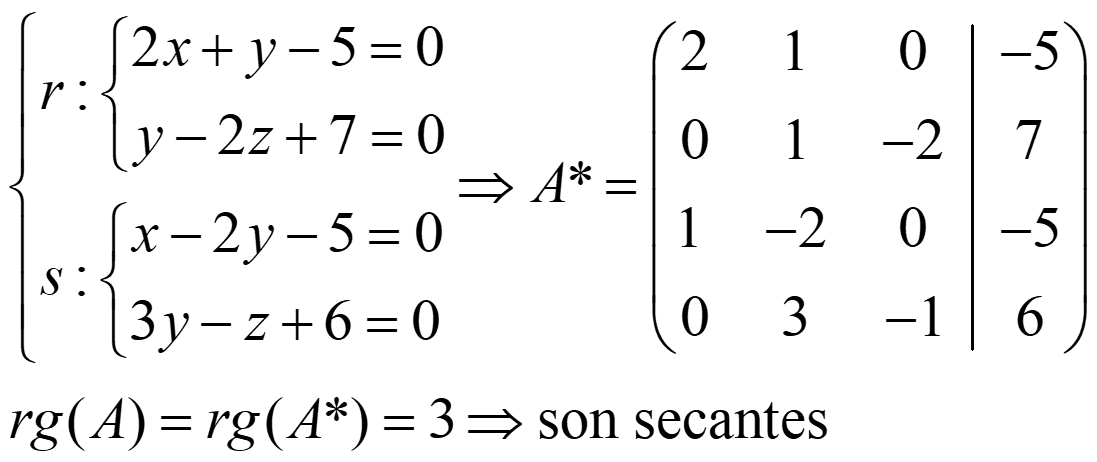
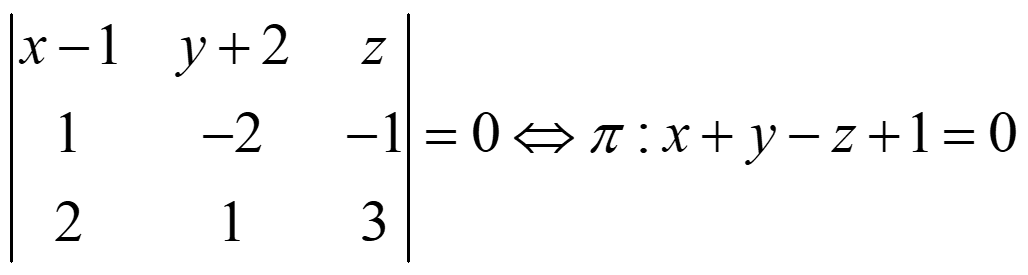
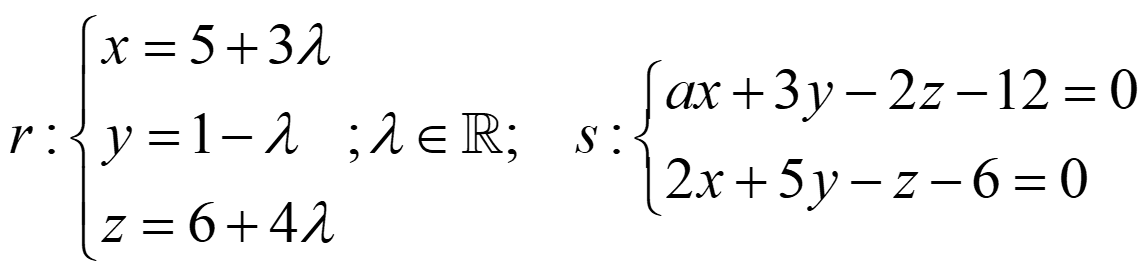
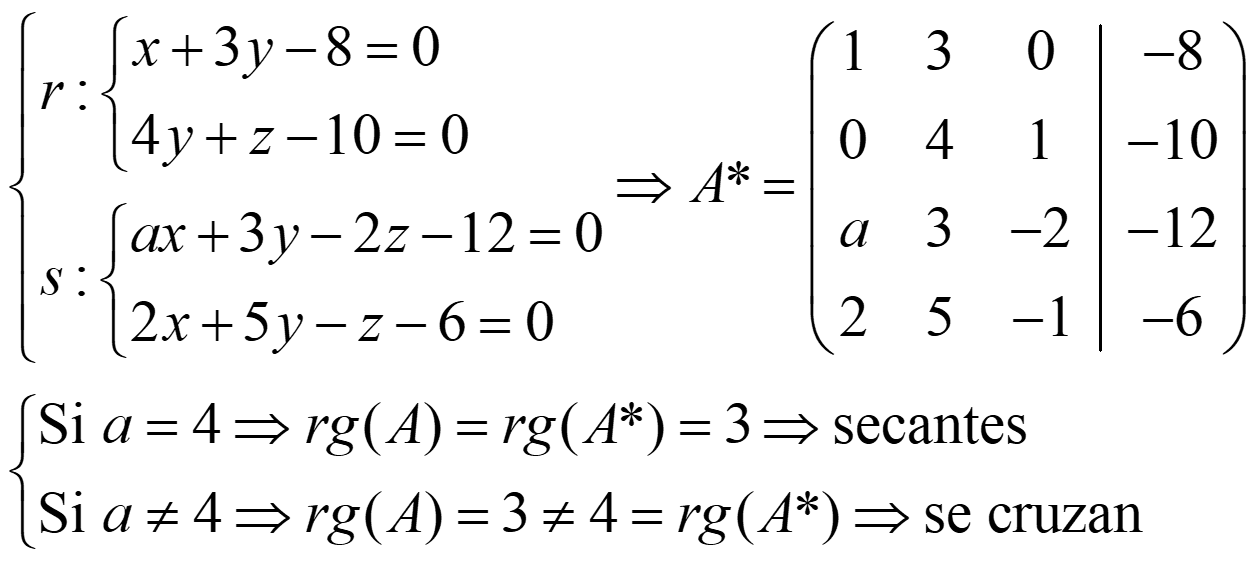
Ejemplo 3. Estudia en función de a, la posición relativa de estas rectas:

Ejemplo 4. Encuentra la recta t₁ que pasa por el punto P(1,0,-1) y corta a r y s:

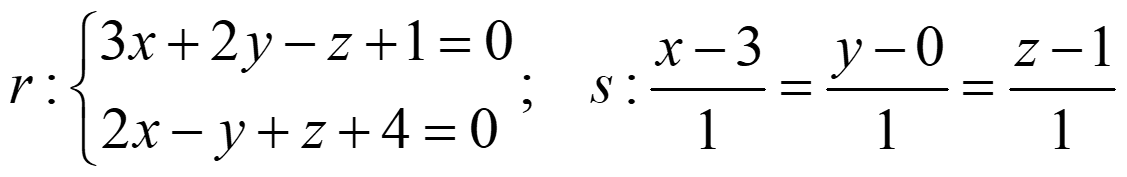
Encuentra también la ecuación de otra recta, t₂, perpendicular a ambas.

Para obtener t₁ buscamos dos planos que la contengan: uno con r y P y otro con s y P:

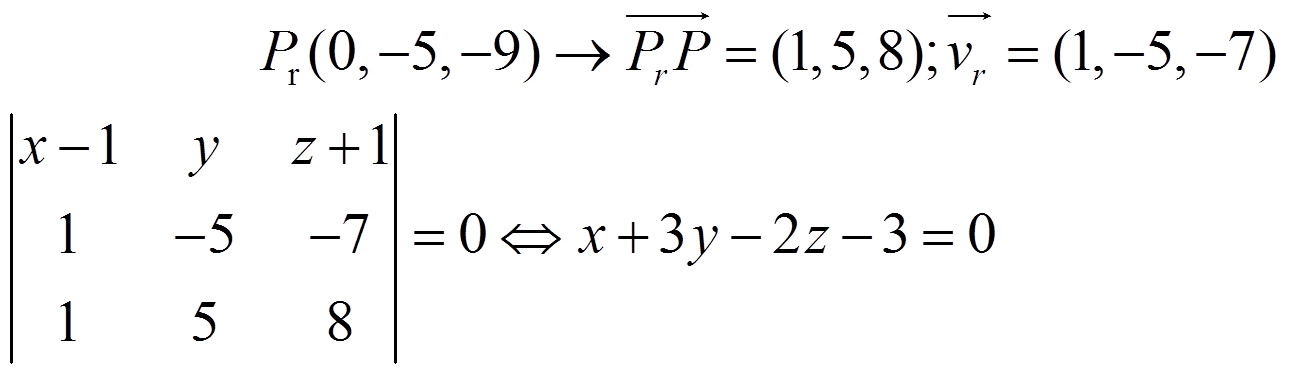
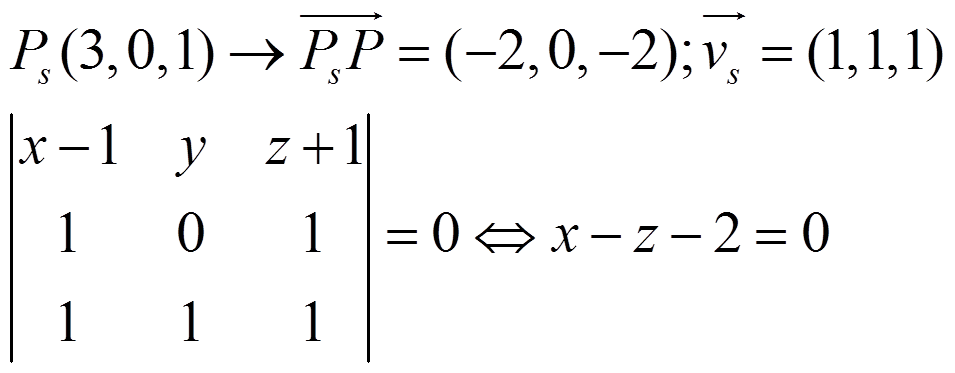
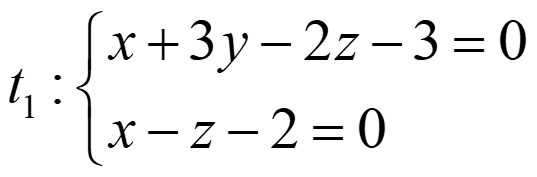
Para t₂, buscamos su vector director como:

Entonces, buscamos la ecuación de dos planos que la contengan, uno con r y w y otro con s y w:

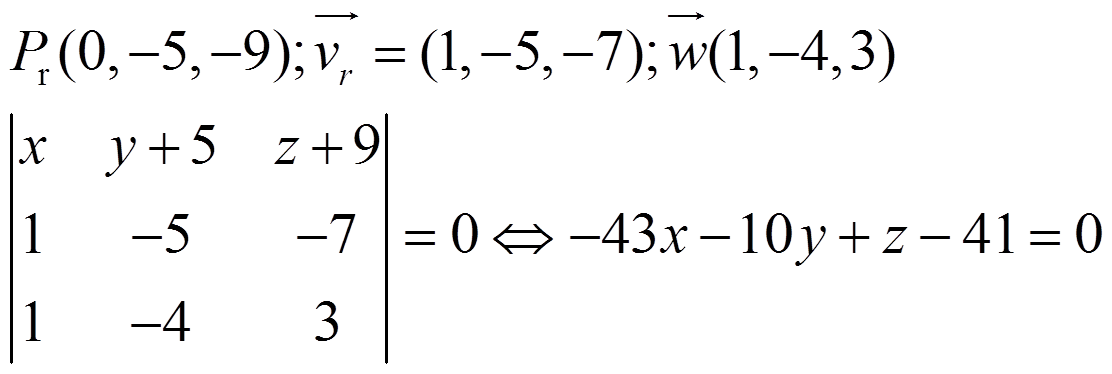
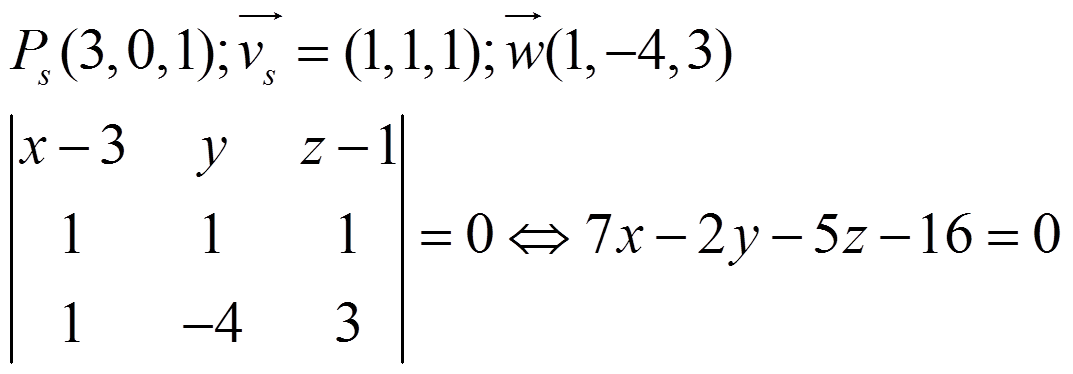
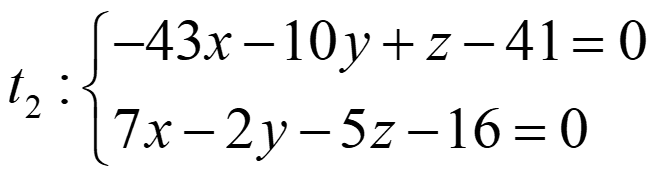
Ejemplo 5. Encuentra la ecuación del punto simétrico a:

· el punto P(-1,1,-1) respecto a la recta:

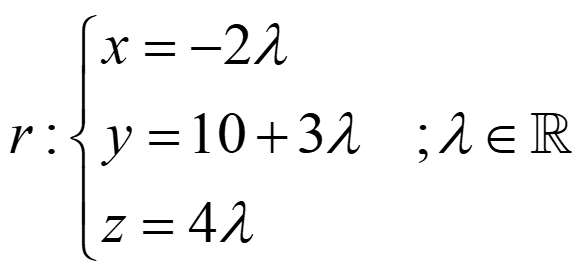
· el punto Q(2,2,-3) respecto al plano π: 3x – y + 2z – 8 = 0

Para el primero, debemos encontrar el punto A. Para ello, buscamos el plano π’ perpendicular a r que pasa por P:

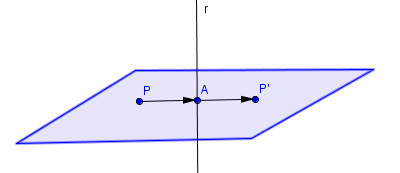
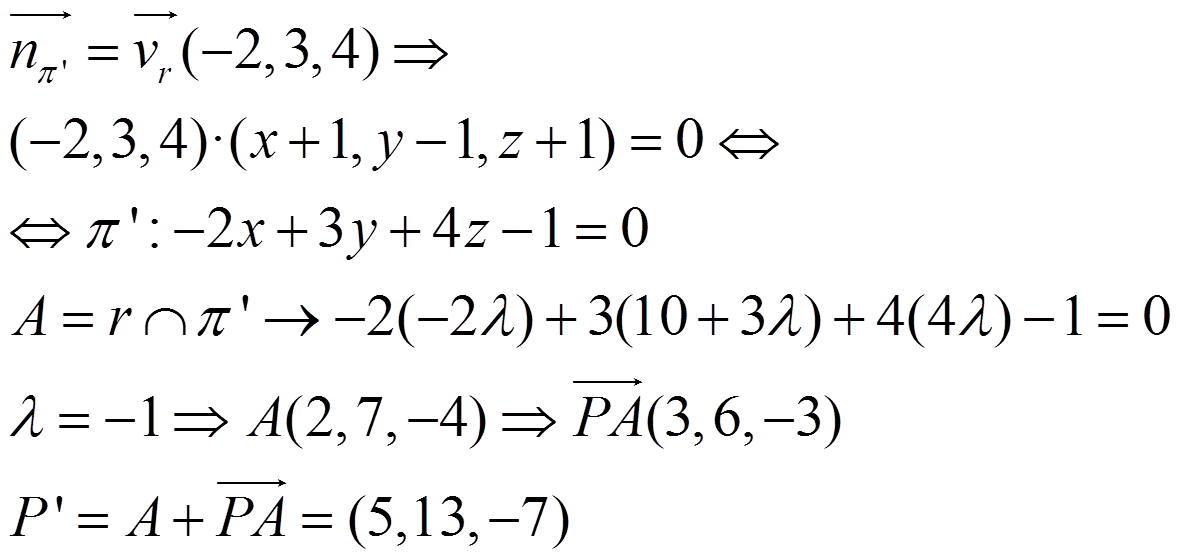
Para el segundo, debemos encontrar B. Para ello, buscamos la recta s perpendicular a π que pasa por Q:

Ejercicios

1.-

a) Sean los puntos P(4, 2, 3) y Q(2, 0,-5). Encuentra la ecuación del plano π que hace que Q sea el punto simétrico de P respecto al plano π.

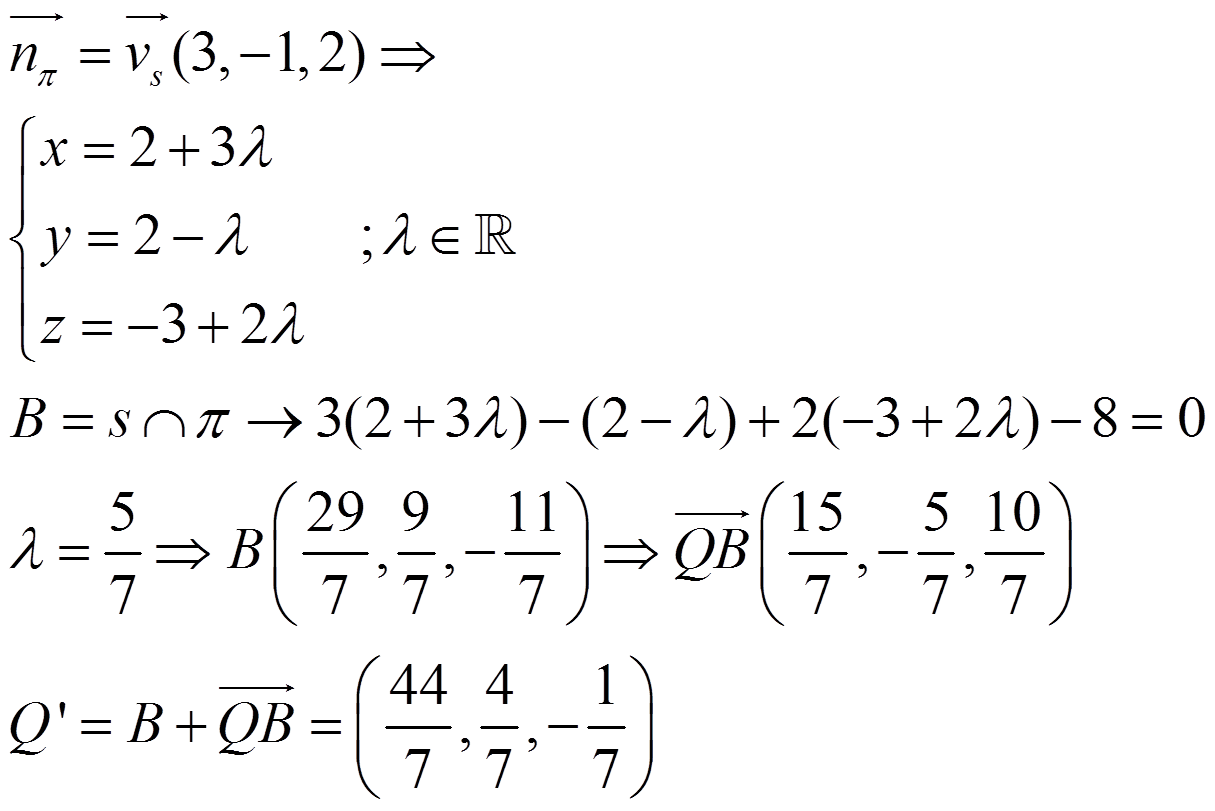
b) Calcula el valor de λ€R que cumpla que el plano determinado por los puntos P, Q, y R(λ,1,0) pase por el origen.

2.- Sean los planos: π: ax + 2y + z - 4 = 0 (a€R) y π´: 2x - 4y - 2z - b = 0 (b€R).

a) Encuentra los valores de a y b que hace que π y π' sean coincidentes.

b) Encuentra los valores de a y b que hace que π y π' sean paralelos no coincidentes.

c) Encuentra los valores de a y b que hace que π y π' sean perpendiculares.

Soluciones: 1) a) x + y + 4z = 0; b) λ = 13/5; 2) a = -1, b = -8; b) a = -1, b ≠ -8; c) a = 5