Para determinar una recta necesitamos un punto y un vector, llamado vector director:
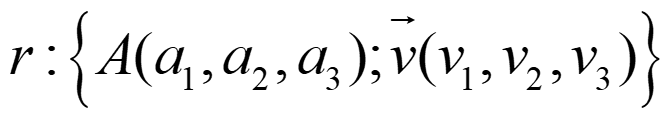
![]()
Pasamos a coordenadas

Si despejamos λ e igualamos:
![]()
Haciendo el producto en cruz y simplificando en dos de ellas obtenemos:

Para determinar un plano necesitamos un punto y dos vectores linealmente independientes (sus vectores directores):
![]()
![]()
Pasamos a coordenadas:
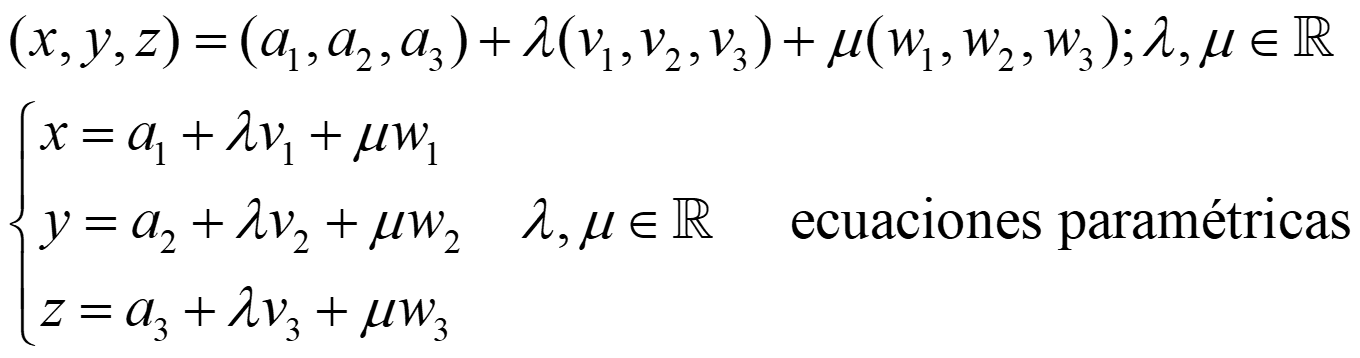

Si tenemos:
donde n es un vector normal, es decir, un vector ortogonal a todo vector que tiene la dirección de π. Entonces:
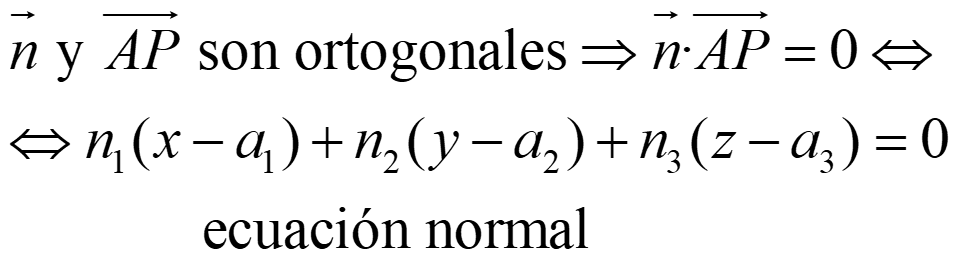
NOTA:
![]()
A. DOS PLANOS
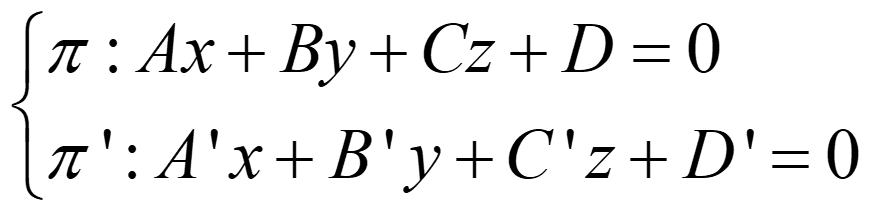
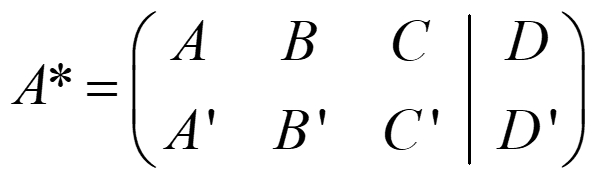
- Si rg(A)=rg(A*)=1 → coincidentes
- Si rg(A)=1≠2=rg(A*) → paralelos
- Si rg(A)=rg(A*)=2 → secantes
B. UN PLANO Y UNA RECTA
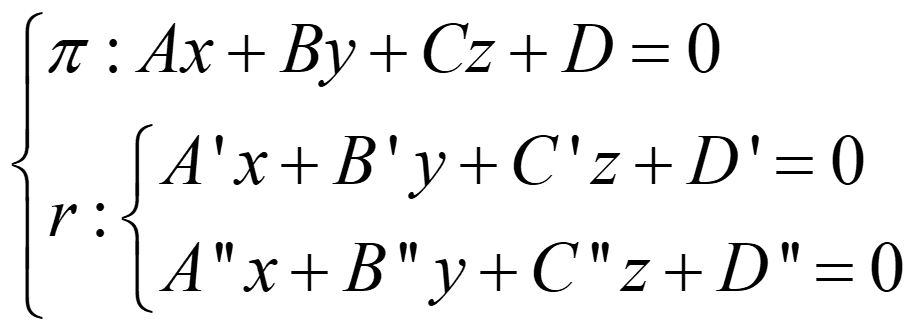
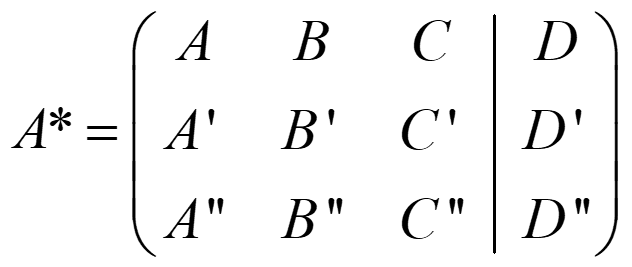
- Si rg(A)=rg(A*)=2 → recta contenida en el plano
- Si rg(A)=2≠3=rg(A*) → paralelos
- Si rg(A)=rg(A*)=3 → secantes
C. DOS RECTAS
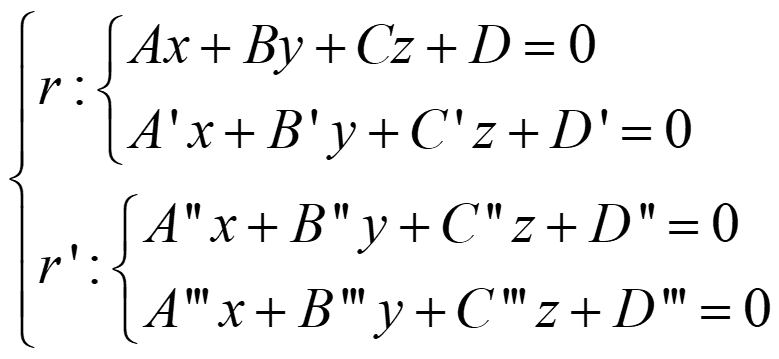
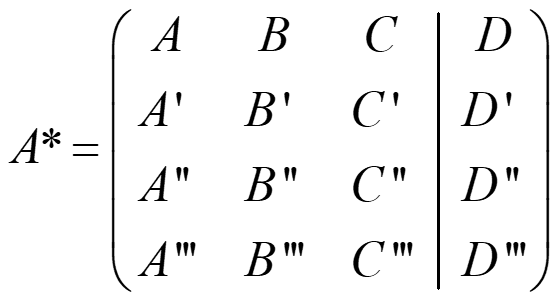
- Si rg(A)=rg(A*)=2 → coincidentes
- Si rg(A)=2≠3=rg(A*) → paralelas
- Si rg(A)=rg(A*)=3 → secantes
- Si rg(A)=3≠4=rg(A*) → se cruzan
D. TRES PLANOS
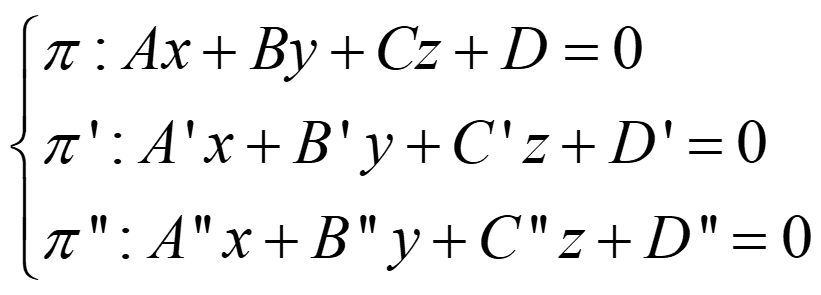
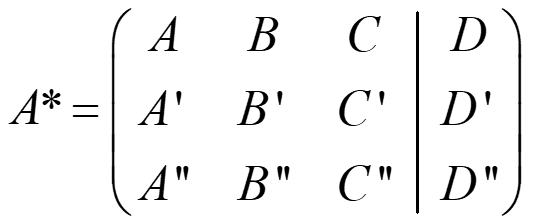
- Si rg(A)=rg(A*)=1 → coincidentes
- Si rg(A)=1≠2=rg(A*) → Dos coincidentes y uno paralelo o los tres paralelos
- Si rg(A)=rg(A*)=2 → o bien se cortan en una recta o dos son coincidentes y el otro se corta con ellos en una recta
- Si rg(A)=2≠3=rg(A*) → o bien dos son paralelos y el otro secante o forman un prisma triangular
- Si rg(A)=rg(A*)=3 → se cortan en un punto
El haz de planos secantes que contienen a una recta r
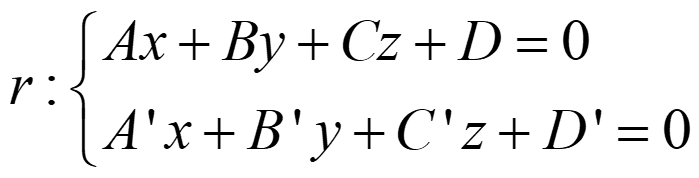
es:
![]()
o:
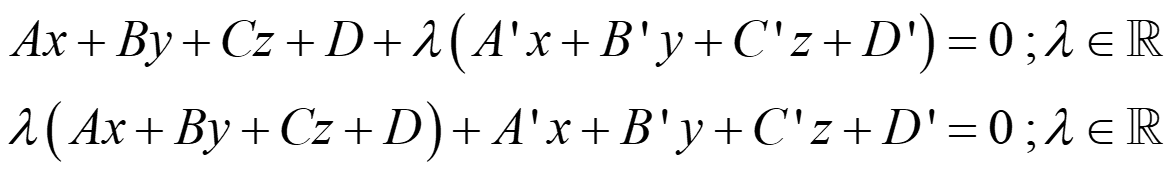
El haz de planos paralelos al plano π
![]()
es
![]()