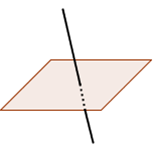
A.DOS PLANOS
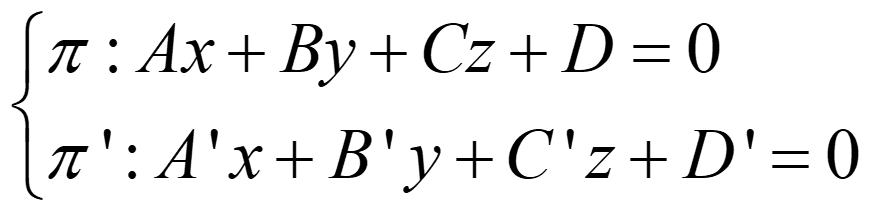
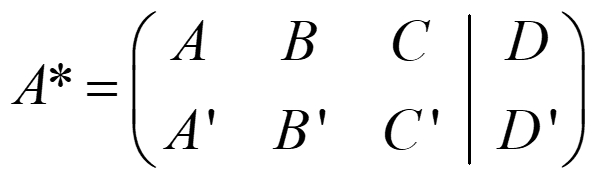
- Si rg(A)=rg(A*)=1 → coincidentes
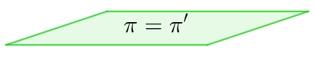
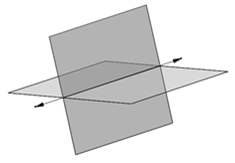
- Si rg(A)=1≠2=rg(A*) → paralelos

- Si rg(A)=rg(A*)=2 → secantes
Ejemplo 1:
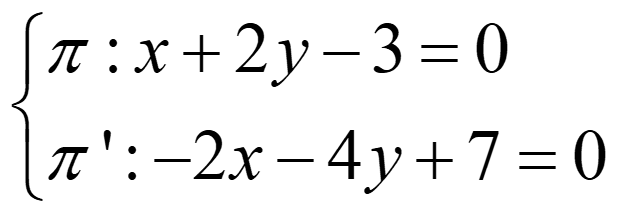
rg(A)=1≠2=rg(A*) → paralelos
Ejemplo 2:
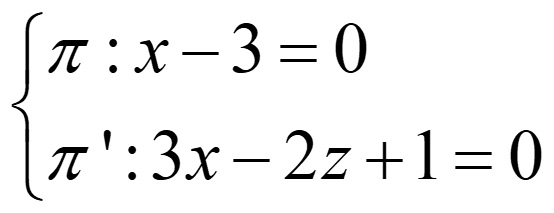
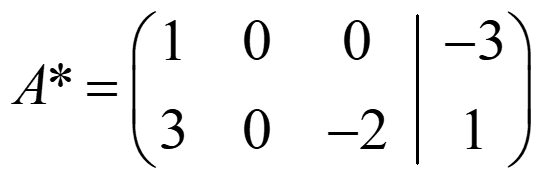
rg(A)=rg(A*) =2 → secantes
B. UN PLANO Y UNA RECTA
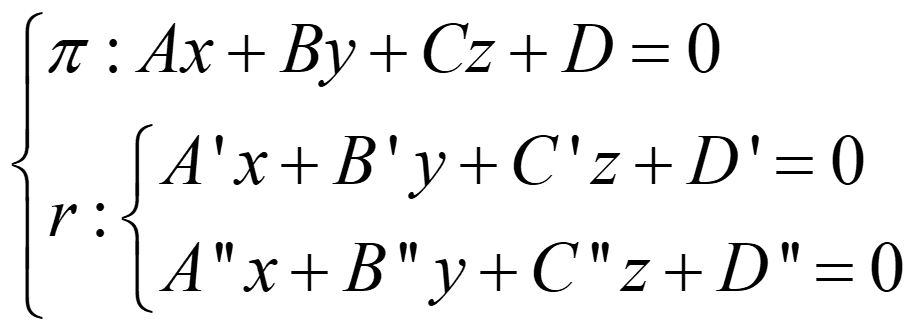
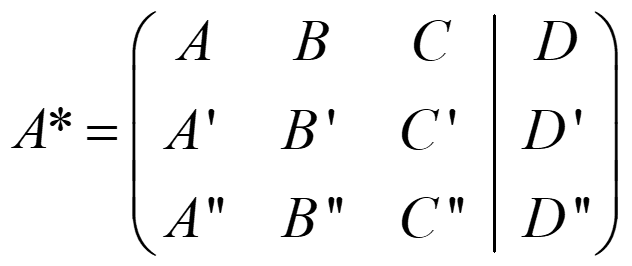
- Si rg(A)=rg(A*)=2 → recta contenida en el plano
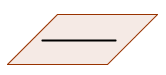
- Si rg(A)=2≠3=rg(A*) → paralelos
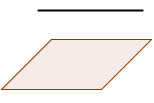
- Si rg(A)=rg(A*)=3 → secantes
Ejemplo 3:
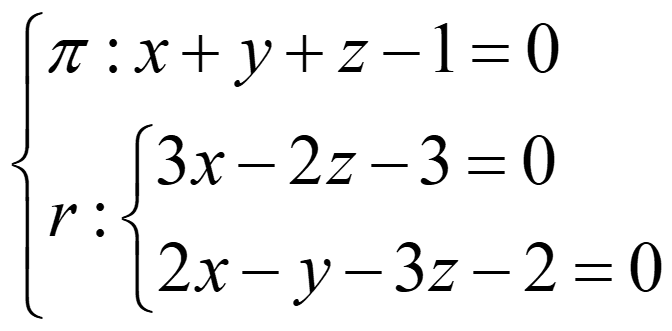
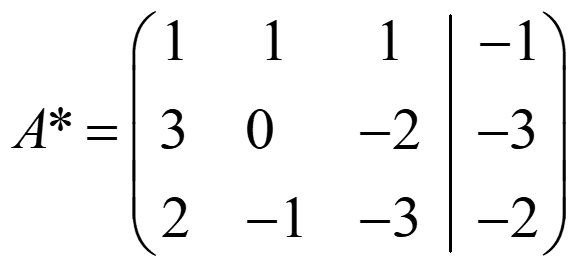
rg(A)=rg(A*)=2 → recta contenida en el plano
Ejemplo 4:
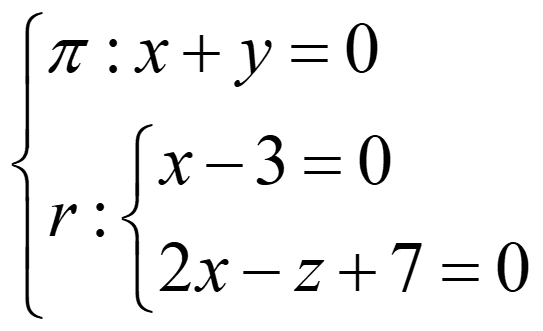
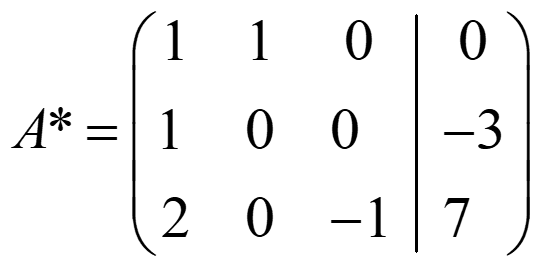
rg(A)=rg(A*) =3 → secantes
C. DOS RECTAS
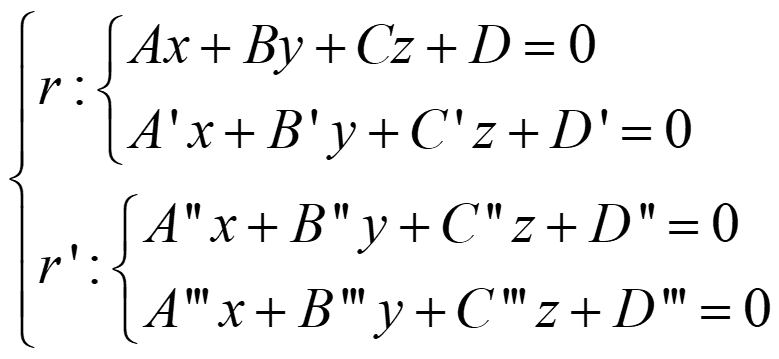
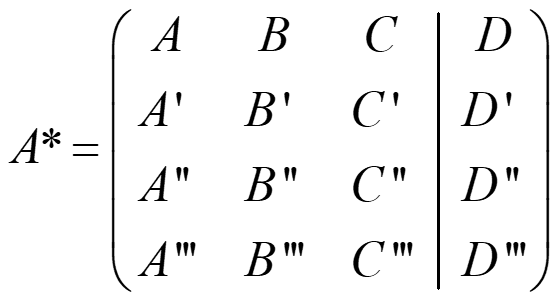
- Si rg(A)=rg(A*)=2 → coincidentes
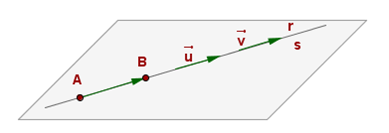
- Si rg(A)=2≠3=rg(A*) → paralelas
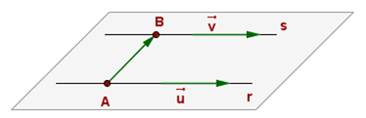
- Si rg(A)=rg(A*)=3 → secantes
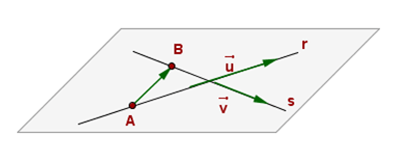
- Si rg(A)=3≠4=rg(A*) → se cruzan

Ejemplo 5:
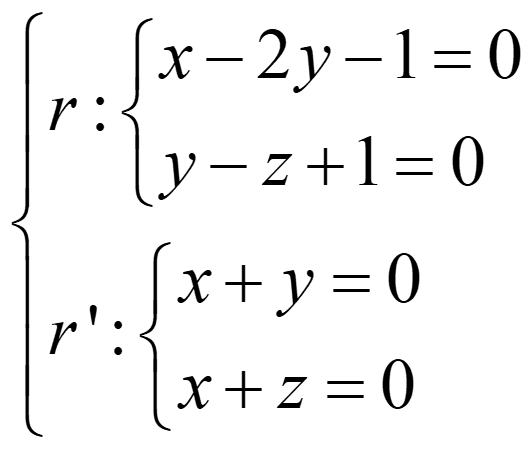
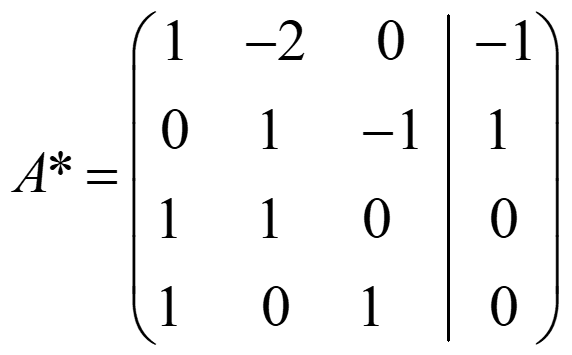
rg(A)=3≠4=rg(A*) → se cruzan
Ejemplo 6:
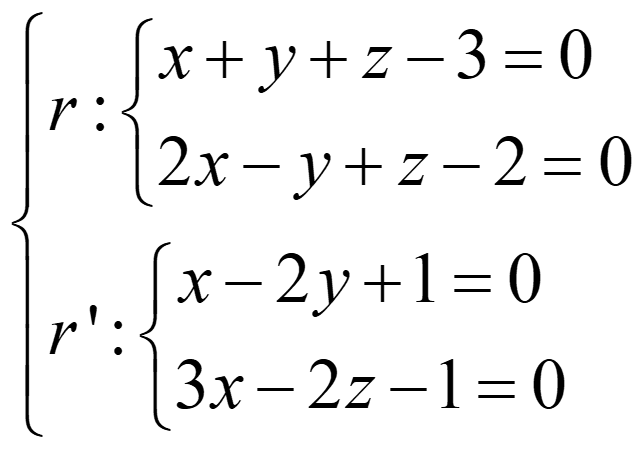

rg(A)=rg(A*) =3 → secantes
D. TRES PLANOS
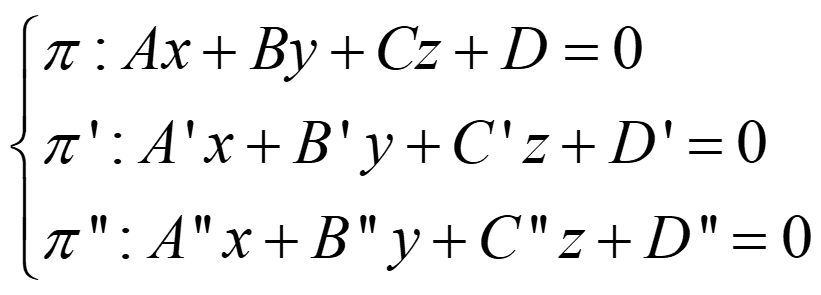
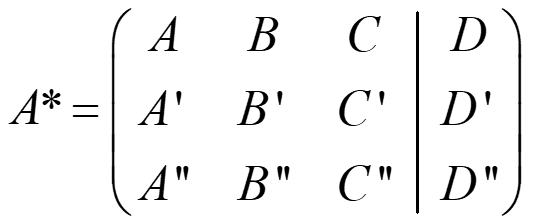
- Si rg(A)=rg(A*)=1 → coincidentes
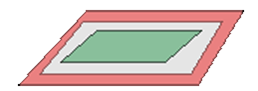
- Si rg(A)=1≠2=rg(A*) → Dos coincidentes y uno paralelo o los tres paralelos
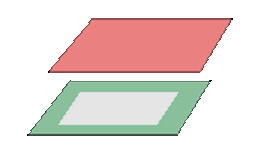
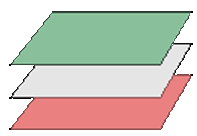
- Si rg(A)=rg(A*)=2 → o bien se cortan en una recta o dos son coincidentes y el otro se corta con ellos en una recta
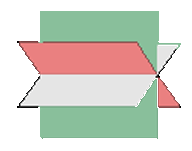
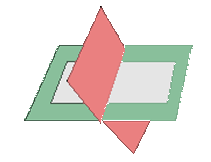
- Si rg(A)=2≠3=rg(A*) → o bien dos son paralelos y el otro secante o forman un prisma triangular
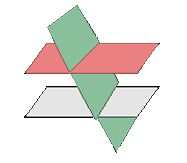

- Si rg(A)=rg(A*)=3 → se cortan en un punto
Ejemplo 7:
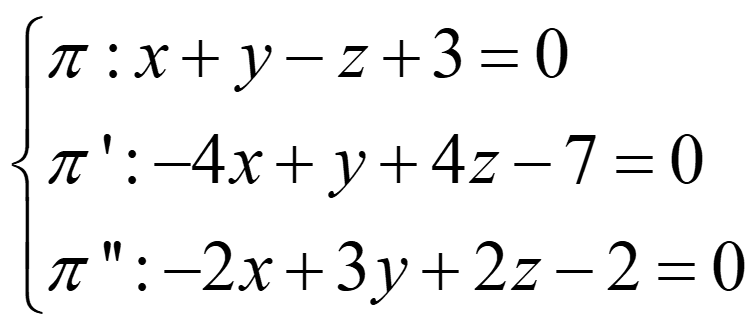
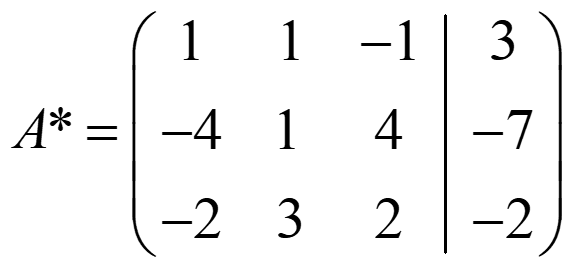
rg(A)=2≠3=rg(A*)→ forman un prisma
Ejemplo 8:
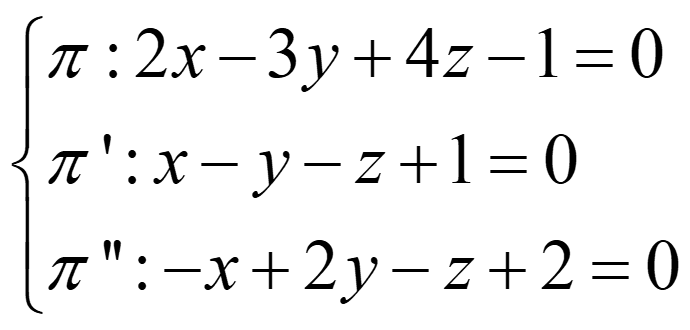
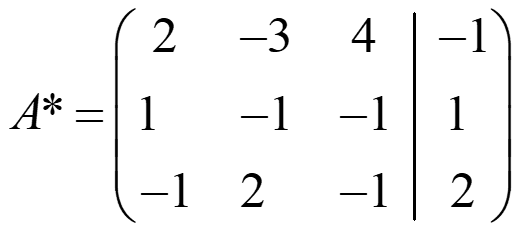
rg(A)=rg(A*) =3 → secantes
Ejercicios
1.- Estudia la posición relativa del plano π: x + 2y - 1 = 0 y la recta r:
![]()
2.- Estudia la posición relativa de las rectas r y s:
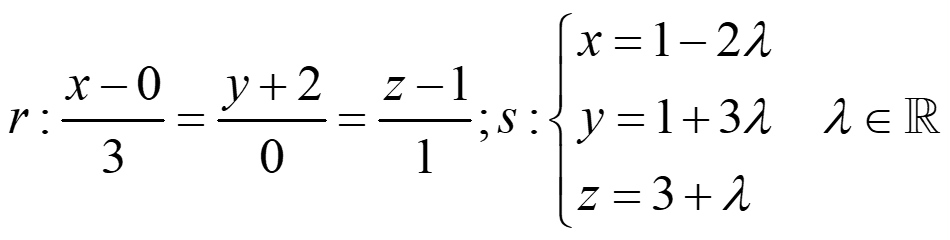
Soluciones: 1) Paralelas; 2) Secantes