Un conjunto de vectores u1,u2,…,un se dice que son linealmente dependientes si existen k1,k2,…,knЄR, tales que:
k1u1 + k2u2 +….+ knun= 0 (vector) con algúnki ≠ 0
Es decir, uno de ellos es combinación lineal de los otros. En caso contrario, se dice que son linealmente independientes.
Se dice que un conjunto de vectores es un sistema generador si todos los vectores se pueden expresar como combinación lineal de esos vectores.
Una base es un conjunto de vectores linealmente independientes que es sistema generador.
En R3 , B = {u1, u2, u3} es una base si:
–Son linealmente independientes
–Son sistema generador, es decir, cada vector v de R3 se puede expresar como v = λ1u1 + λ2u2 + λ3u3. (λ1, λ2, λ3) son las coordenadas de v con respecto a la base B.

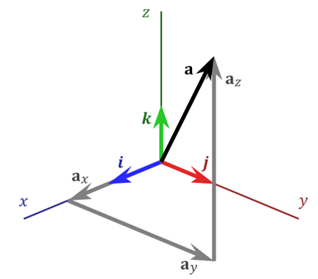
Y siempre existe un vector equipolente
![]()
el vector de posición de P
Para calcular el módulo usamos el teorema de Pitágoras:
![]()
Entonces, se prueba que:
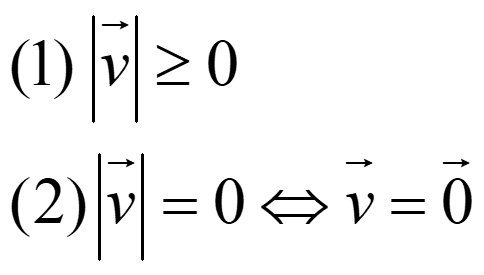
Si |v| = 1, se dice que es un vector unitario.
Las operaciones con vectores en coordenadas serían:
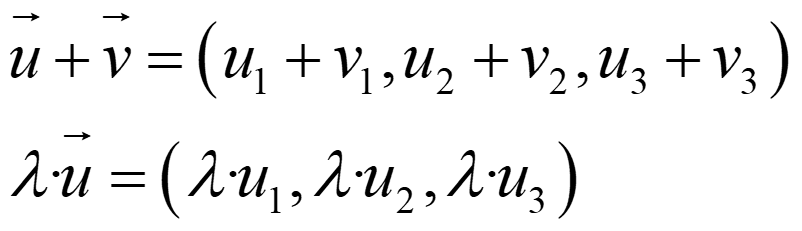
Ejercicios
1.- Si u(3,-2,1), v(1,3,-2), A(1,t,2), B(-3,3,0):
a) Calcula el módulo de u.
b) Calcula t si AB(-4,-2,-2).
c) Calcula u + v, 2u - 5v
2.- Decide si los siguientes conjuntos de vectores son linealmente dependientes, linealmente independientes, sistemas generadores y/o bases:
a) B1={(1,0,0),(1,1,0),(1,1,1)}
b) B2={(1,0,0),(0,1,0),(0,0,1),(1,1,1)}
c) B3={(1,1,1),(1,-1,3),(-1,3,-5)}
Soluciones:
1.- a)|u|= √14; b) 5; c) u + v = (4,1,-1); 2u - 5v = (1,-19,12)
2.- a) Base, sistema generador y linealmente independientes; b) Linealmente dependientes y sistema generador; c) Linealmente dependientes