Sean u y v vectores linealmente independientes. ¿Cómo determinamos todos los vectores ortogonales a ambos?

Podemos suponer que:

Este vector se denota
y es el producto vectorial de u y v
Entonces:
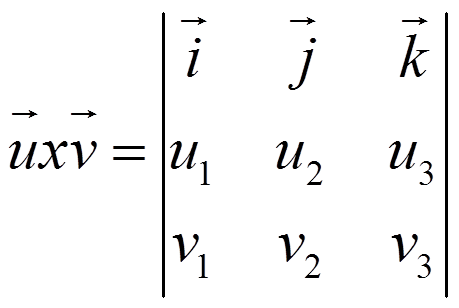
- Su módulo es:
- Su dirección es la perpendicular a u y v.
- Su sentido se determina por la “regla del sacacorchos” o la “regla de la mano derecha”: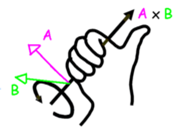
Propiedades:

(vii) El área del paralelogramo formado por u y v es el módulo de su producto vectorial.
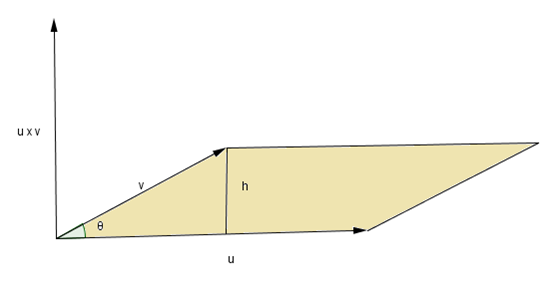
Demostración:
![]()
Ejercicio. Sean A(1,1,1),B(2,-1,0),C(3,3,-2). Calcula:
a) ABxAC
b) Un vector unitario ortogonal a AB y AC
c) El área del paralelogramo definido por los vectores AB y AC
d) El área del triángulo ABC
Soluciones: a) (-4,1,-2); b) (-4√21/21,√21/21,-2√21/21); c) √21u2; d) √21/2u2