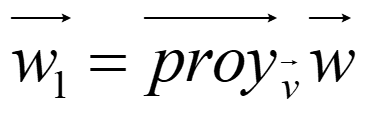Un vector es un segmento orientado. Lo representamos AB, donde A es el origen y B el extremo.
Las características de un vector son:
–Módulo |AB|: la longitud del segmento.
–Dirección: la de la recta que lo contiene y sus paralelas.
–Sentido: el que va desde el origen al extremo.

Cada vector queda definido por su módulo dirección y sentido.
Se dice que dos vectores son equipolentes si tienen el mismo módulo dirección y sentido. El conjunto de vectores equipolentes entre sí se llama vector libre y su módulo, dirección y sentido es el de cualquier vector del conjunto.
Para sumar dos vectores, u y v, unimos el extremo de u con el origen de v y entonces, u + v tiene como origen el de u y como extremo el de v.

El opuesto de un vector v, es otro vector, -v, con el mismo módulo y dirección y sentido opuesto.
Para restar dos vectores, u y v, sumamos u y –v.

–módulo:|λ|·|v|
–la misma dirección que v
–con el mismo sentido si λ > 0, y sentido opuesto si λ < 0.
–(i) Propiedad conmutativa: u + v = v + u
–(ii) Propiedad asociativa: u + (v + w) = (u + v) + w
–(iii) Elemento neutro:
![]()
–(iv) Elemento opuesto:
![]()
–(v) Propiedades distributivas:
(λ +µ)·u= λ·u + µ·u λ(u+v) = λ·u + λ·v
–(vi)
![]()
–(vii) Desigualdad triangular: |u + v| ≤ |u| + |v|
Con todas estas propiedades,
![]()
tiene una estructura de espacio vectorial.
Un conjunto de vectores u1,u2,…,un se dice que son linealmente dependientes si existen k1,k2,…,knЄR, tales que:
k1u1 + k2u2 +….+ knun= 0 (vector) con algún ki ≠ 0
Es decir, uno de ellos es combinación lineal de los otros. En caso contrario, se dice que son linealmente independientes.
Se dice que un conjunto de vectores es un sistema generador si todos los vectores se pueden expresar como combinación lineal de esos vectores.
Una base es un conjunto de vectores linealmente independientes que es sistema generador.

Y siempre existe un vector equipolente
![]()
el vector de posición de P
Para calcular el módulo usamos el teorema de Pitágoras:
![]()
Entonces, se prueba que:

Si |v| = 1, se dice que es un vector unitario.
Las operaciones con vectores en coordenadas serían:

El producto escalar de dos vectores, u y v, es el número real: u·v = u1·v1 + u2·v2 + u3v3
Propiedades:
- Propiedad conmutativa: u·v = v·u
- Propiedad asociativa con respecto al producto por un escalar: (k·u)·v = k·(u·v) k€R
- Propiedad distributiva: u·(v + w) = u·v + u·w
- ![]()
- v·v = |v|2
- Desigualdad de Cauchy-Schwartz: |u·v| ≤ |u|·|v|

Entonces
![]()
Dos vectores, u y v, se dice que son ortogonales si u·v=0
Propiedades:
Sean v y w dos vectores no nulos. Si w=w1+w2 con w1 paralelo a v y w2 ortogonal a v, decimos que w1 es la proyección ortogonal de w sobre v y w2 su componente ortogonal.

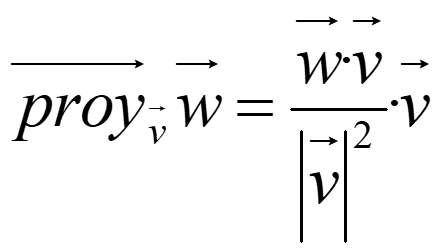
NOTA. Si u es un vector unitario
![]()
Entonces, el producto escalar por un vector unitario, u, mide la longitud de la proyección ortogonal en la dirección de u.
![]() es el producto vectorial de u y v
es el producto vectorial de u y v

- Su módulo es:


Sean u, v y w vectores. Definimos producto mixto de u, v y w como el número: