Saltar la navegación

Producto escalar

El producto escalar de dos vectores, u y v, es el número real: u·v = u1·v1 + u2·v2 + u3v3

Propiedades:

- Propiedad conmutativa: u·v = v·u

- Propiedad asociativa con respecto al producto por un escalar: (k·u)·v = k·(u·v)      k€R

- Propiedad distributiva: u·(v + w) = u·v + u·w

-

- v·v = |v|2

- Desigualdad de Cauchy-Schwartz: |u·v| ≤ |u|·|v|

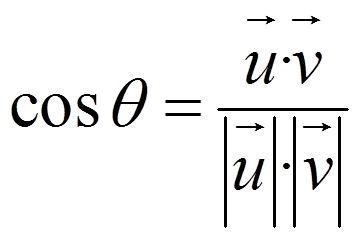
Teorema. Si θ (≤ π) es el ángulo entre u y v, entonces:

Demostración:

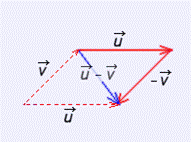
Tma del coseno→ |u-v|2=|u|2+|v|2-2|u||v|cosθ

Por otro lado: (u-v)2=(u-v)(u-v)=u2-uv-vu+v2=|u|2+|v|2-2uv

Igualando: -2uv =-2|u||v|cosθ

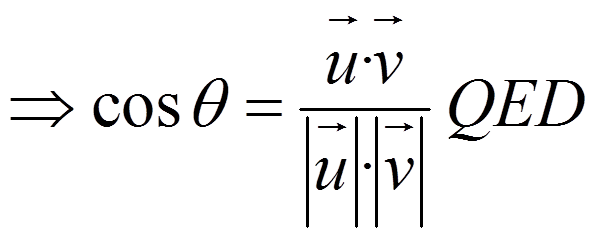
Entonces

Dos vectores, u y v, se dice que son ortogonales si u·v=0

Propiedades: 

–Si u = 0 → u es ortogonal a todos los vectores
 
–Si u,v ≠ 0, entonces: u·v = 0 ↔ θ = π/2
 
Una base ortonormal está formada por vectores unitarios ortogonales entre sí.
Un ejemplo de base ortonormal es la base canónica.

Sean v y w dos vectores no nulos. Si w=w1+w2 con w1 paralelo a v y w2 ortogonal a v, decimos que w1 es la proyección ortogonal de w sobre v y w2 su componente ortogonal.

 

 
Denotamos:
 
Entonces
 
Demostración:

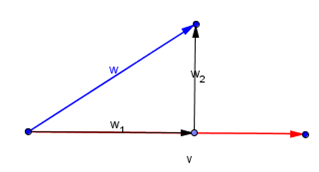
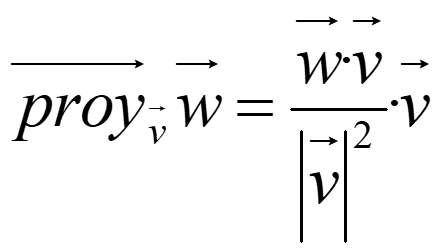
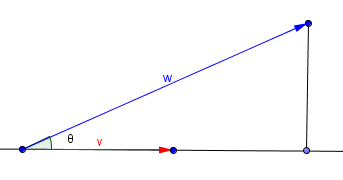
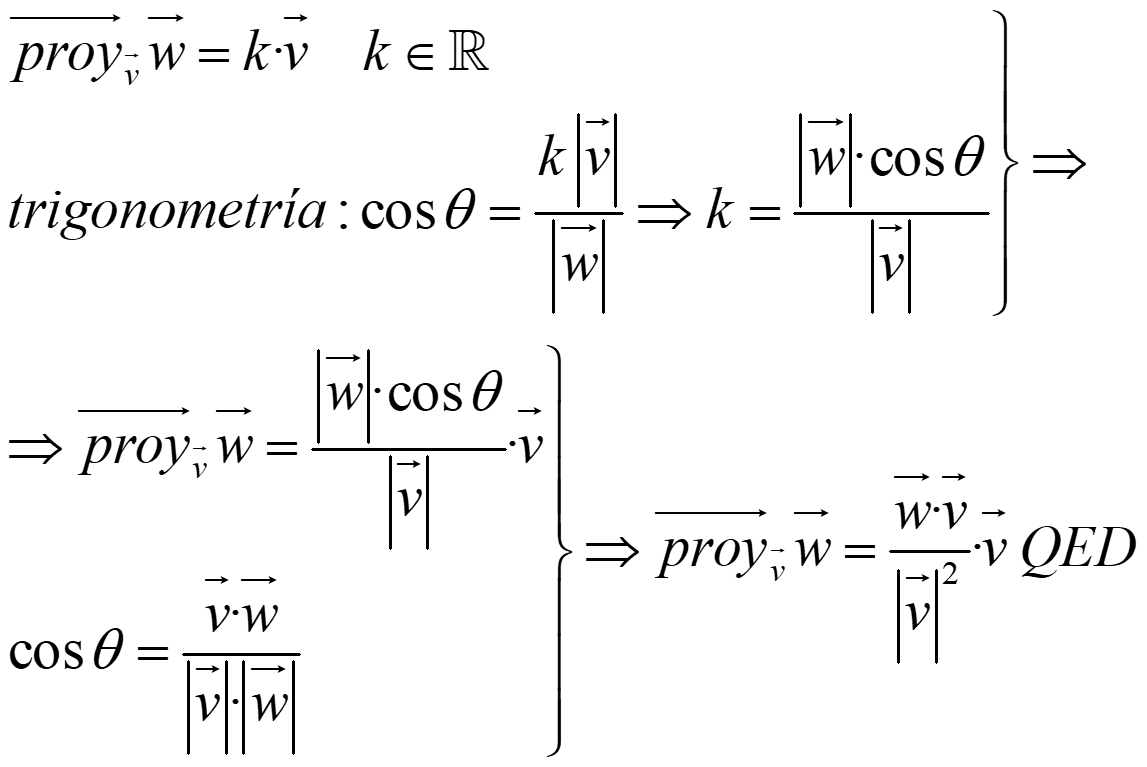
NOTA. Si u es un vector unitario

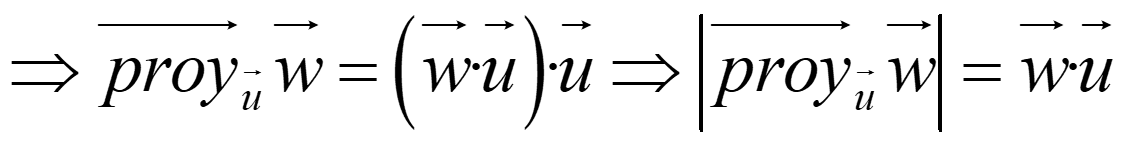
Entonces, el producto escalar por un vector unitario, u, mide la longitud de la proyección ortogonal en la dirección de u.

 
 
Ejercicios
 
1.- Sean u(-1,-1,2) y v(2,-3,1):
 
a) Calcula el ángulo que forman u y v.
 
b) Calcula la proyección ortogonal de u sobre v.
 
2.-Sean los puntos A(1,-5,k), B(3,k,1), C(k,-5,2) los vértices de un triángulo. Encuentra el valor de k que hace que formen un triángulo rectángulo, con el ángulo recto en A.
 
 
 
 
 
Soluciones: 1.- a) 70o53'36''; b) (3/7,-9/14,3/4); 2.- k =  0, k = 1