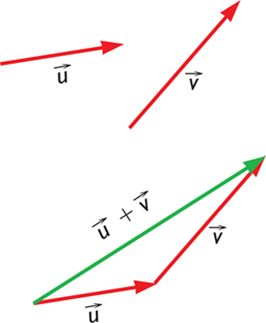
Para sumar dos vectores, u y v, unimos el extremo de u con el origen de v y entonces, u + v tiene como origen el de u y como extremo el de v.
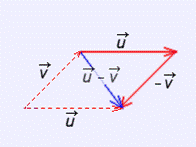
El opuesto de un vector v, es otro vector, -v, con el mismo módulo y dirección y sentido opuesto.
Para restar dos vectores, u y v, sumamos u y –v.
La multiplicación de un vector v por un escalar λ (λЄR), es otro vector, λv, con:
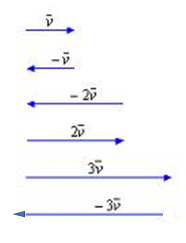
–módulo:|λ|·|v|
–la misma dirección que v
–con el mismo sentido si λ > 0, y sentido opuesto si λ < 0.
PROPIEDADES. Sean u, v, w vectores libres y λ, µ números reales
–(i) Propiedad conmutativa: u + v = v + u
–(ii) Propiedad asociativa: u + (v + w) = (u + v) + w
–(iii) Elemento neutro:
–(iv) Elemento opuesto:
–(v) Propiedades distributivas:
(λ +µ)·u= λ·u + µ·u λ(u+v) = λ·u + λ·v
–(vi)
–(vii) Desigualdad triangular: |u + v| ≤ |u| + |v|
Con todas estas propiedades,
tiene una estructura de espacio vectorial.